Hãy chứng minh rằng điện trở tương đương Rtđ của một đoạn mạch song song chẳng hạn gồm 3 điện trở R 1 , R 2 , R 3 mắc song song với nhau, thì nhỏ...

HD

Hoàng Đức Long

12 tháng 10 2017

Hãy chứng minh rằng điện trở tương đương Rtđ của một đoạn mạch song song chẳng hạn gồm 3 điện trở R 1 , R 2 , R 3 mắc song song với nhau, thì nhỏ hơn mỗi điện trở thành phần ( R t đ < R 1 ; R t đ < R 2 ; R t đ < R 3 ...

Đọc tiếp

#Vật lý lớp 9

1

VT

Vũ Thành Nam

12 tháng 10 2017

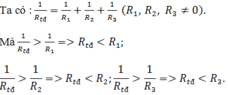
Giải SBT Vật Lí 9 | Giải bài tập Sách bài tập Vật Lí 9

Đúng(1)

TN

tamanh nguyen

12 tháng 11 2021

Cho ba điện trở R1 = R2 = R3 = R mắc song song với nhau. Điện trở tương đương đương Rtđ của đoạn mạch đó có thể nhận giá trị nào trong các giá trị

A. Rtđ = R.

B. Rtđ = 2R.

C. Rtđ = 3R.

D. Rtđ = R/3

#Vật lý lớp 9

1

NT

nguyễn thị hương giang

12 tháng 11 2021

Cho ba điện trở R1 = R2 = R3 = R mắc song song với nhau. Điện trở tương đương đương Rtđ của đoạn mạch đó có thể nhận giá trị nào trong các giá trị

A. Rtđ = R.

B. Rtđ = 2R.

C. Rtđ = 3R.

D. Rtđ = R/3

Giải thích:

$\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}=\dfrac{3}{R}$

$\Rightarrow R_{tđ}=\dfrac{R}{3}\Omega$

Chọn D.

Đúng(3)

ND

Ngyuễn Duy Khang

21 tháng 6 2017

1)khi mắc nối tiếp 2 điện trở R1 và R2 vào HĐT 1,2V thì CĐDĐ chạy qua chúng là 0,12A a) Tính điện trở tương đương của đoạn mạch nối tiếp này b) nếu mắc song song hai điện trở nói trên vào một hiệu điện thế thì dòng điện chạy qua R1 có cường độ I1 gấp 1,5 lần cường độ qua I2 của điện trở R2. Tính R1 và R2 2)hãy chứng minh rằng Rtđ của đoạn mạch song song( chẳng hạn gồm ba điện trở...

Đọc tiếp

#Vật lý lớp 9

2

NK

Như Khương Nguyễn

21 tháng 6 2017

Làm bài khó trước

Bài 2 :

Điện trở tương đương của n đoạn mạch song song là :

$\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+...+\dfrac{1}{R_n}$

Các giá trị $R_{tđ},R_1,R_2,...$có giá trị dương nên:

$\dfrac{1}{R_{tđ}}>\dfrac{1}{R_{R_1}}=>R_{tđ}< R_1$

$\dfrac{1}{R_{tđ}}>\dfrac{1}{R_2}=>R_{tđ}< R_2$

$........$

$\dfrac{1}{R_{tđ}}>\dfrac{1}{R_n}=>R_{tđ}< R_n$

Rtđ của đoạn mạch song song nhau thì nhỏ hơn mỗi điện trở thành phần .

Đúng(0)

NK

Như Khương Nguyễn

21 tháng 6 2017

Bài 1 :

a, $R_{tđ}=R_1+R_2=\dfrac{U}{I}=\dfrac{1,2}{0,12}=10\Omega$

b,

Ta có : $R_1$//$R_2$

$U_1=U_2$

$I_1.R_1=I_2.R_2$

Mà $I_1=1,5I_2$

$1,5I_2.R_1=I_2.R_2$

$=>1,5R_1=R_2\left(1\right)$

Mặt khác ta có ; $R=R_1+R_2=10\left(2\right)$

Từ (1) và (2) có ;

$R_1+1,5R_1=10$

$2,5R_1=10=>R_1=4\Omega$

$R_2=6\Omega$

Vậy ...

Đúng(0)

TT

Tống Thanh Hà

14 tháng 9 2016

hãy chứng minh rằng điện trở tương đương $_{R_{tđ}}$ của một đoạn mạch song song , chẳng hạn gồm 3 điện trở $_{R_1}$,$_{R_2}$ ,$_{R_3}$ mắc song song với nhau , thì nhỏ hơn mỗi điện trở thành phần

( $_{R_{tđ}}$ < $_{R_1}$ ; $_{R_{tđ}}$ <$_{R_2}$ ; $_{R_{tđ}}$<$_{R_3}$)

#Vật lý lớp 9

3

NK

Nguyễn Khánh Vi

19 tháng 9 2016

Pạn dựa vào địh nghĩa điện trở tươg đươg trog đoạn mạch song2 mà giải bt này nké

Đúng(0)

NK

Nguyễn Khánh Vi

19 tháng 9 2016

Điện học lớp 9

Đúng(0)

V

vvvvvvvv

11 tháng 11 2019

chọn câu sai A. Điện trở tương đương R của n điện trở r mắc nối tiếp : R=n.r B.điện trở tương đương R của n điện trở r mắc song song : R=$\frac{r}{n}$ C.Điện trở tương đương của mạch mắc song song nhỏ hơn điện trở mỗi thành phần D.Trong đoạn mạch mắc song song cường độ dòng điện chạy qua các điện trở là bằng...

Đọc tiếp

#Vật lý lớp 9

3

LT

Lê Thị Hà Trang

11 tháng 11 2019

Câu sai :D

Đúng(0)

NT

Nguyễn Thị Thanh Nhàn

11 tháng 11 2019

Đáng ra phải là chọn câu đúng chứ:

A. Điện trở tương đương R của n điện trở r mắc nối tiếp : R=n.r

B.điện trở tương đương R của n điện trở r mắc song song : R= $rnrn$

C.Điện trở tương đương của mạch mắc song song nhỏ hơn điện trở mỗi thành phần

D.Trong đoạn mạch mắc song song cường độ dòng điện chạy qua các điện trở là bằng nhau

Đúng(0)

LK

LÊ KHÁNH NGUYÊN

13 tháng 11 2021 - olm

Cho ba điện trở R1 = R2 = R3 = R mắc song song với nhau . Điện trở tương đương Rtđ của đoạn mạch đó có thể giá trị nào trong các giá trị .

A. Rtđ = R

B. Rtđ =2R

C. Rtđ = 3R

D. Rtđ = R/3

#Vật lý lớp 9

2

US

Unirverse Sky

13 tháng 11 2021

Cho ba điện trở R1 = R2 = R3 = R mắc song song với nhau . Điện trở tương đương Rtđ của đoạn mạch đó có thể giá trị nào trong các giá trị .

A. Rtđ = R

B. Rtđ =2R

C. Rtđ = 3R

D. Rtđ = R/3

Đúng(0)

HT

Hoàng Thị Minh Nguyệt

18 tháng 11 2021

Chọn đáp án C

Đúng(0)

MD

Mal Dairy

21 tháng 2 2021

Cho ba điện trở R₁ = R₂= R₃ = R mắc song song với nhau. Điện trở tương đương đương R_tđ của đoạn mạch đó có thể nhận giá trị nào trong các giá trị

#Vật lý lớp 9

2

ND

Nguyễn Duy Khang

21 tháng 2 2021

$\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}=\dfrac{3}{R}\\ \Rightarrow R_{tđ}=\dfrac{R}{3}$

Đề chưa rõ lắm nhé, bạn dựa vào để tính ...

Đúng(2)

NP

Nguyễn Phương Thúy (tina)

21 tháng 2 2021

1\Rtđ=1\R1+1\R2+1\R3

Đúng(1)

HD

Huỳnh đạt

2 tháng 11 2023

Một đoạn mạch gồm 2 điện trở R1=6 om ×R=3 om mắc song song với nhau vào hai điểm có hiệu điện thế 6V A) Tính điện trở tương đương của đoạn mạch

#Vật lý lớp 9

1

H9

HT.Phong (9A5)

CTVHS

2 tháng 11 2023

Điện trở tương đương của mạch là:

$R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{6\cdot3}{6+3}=\dfrac{18}{9}=2\Omega$

Đúng(1)

CY

Can You Find Me?

5 tháng 1 2022

Cho đoạn mạch gồm 2 điện trở R1 = 6 R= 6Ω mắc song song với nhau, điện trở tương đương của đoạn mạch là?

#Vật lý lớp 9

2

R

Rhider

5 tháng 1 2022

tóm tắc

$R_1=R_2=6\left(\text{ Ω}\right)$

$R_{tđ}=?$

Giải

Điện trở tương đương của đoạn mạch là:

$\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{6.6}{6+6}=3\left(\text{Ω}\right)$

Đáp số : $R_{tđ}=3\text{Ω}$

Đúng(2)

MN

Minh Nhân

5 tháng 1 2022

$R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{6\cdot6}{6+6}=3\left(\text{Ω}\right)$

Đúng(2)

D

dfgtrdtrdt

22 tháng 9 2020

Đoạn mạch AB gồm các điện trở R₁, R₂,R₃,..,R_n(n điện trở, n>2, n nguyên) mắc song song nhau. CMR giá trị điện trở tương đương của đoạn mạch nhỏ hơn trị số mỗi điện trở thành phần

#Vật lý lớp 9

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP