Cho tam giác ABC và điểm M thỏa mãn M A → = M B → + M C → . Khẳng định nào sau đây đúng?
A.Ba điểm C ; M ; B thẳng hàng.
B. AM là phân giác trong của góc B A C ^ .
C. A; Mvà trọng tâm tam giác ABC thẳng hàng.
D. A M → + B C → = 0 → .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2 M A → + M B → = C A → ⇔ 2 M A → + M B → = C M → + M A → .
⇔ M A → + M B → = − M C → ⇔ M A → + M B → + M C → = 0 → . (*)
Đẳng thức (*) suy ra M là trọng tâm của tam giác ABC.
Chọn D.

Đáp án C.
Gắn hệ trục tọa độ Oxyz, với O(0;0;0) là trung điểm của AB => OC= 3
Khi đó
![]()
![]()
![]()
![]()
⇒ x 2 + ( y + 1 ) 2 + z 2 + x 2 + ( y - 1 ) 2 + z 2 + 2 ( x - 3 ) 2 + 2 y 2 + 2 z 2 = 12
![]()
![]()
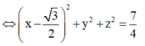
Vậy tập hợp các điểm M là một mặt cầu có bán kính
R
=
7
2

Đáp án A
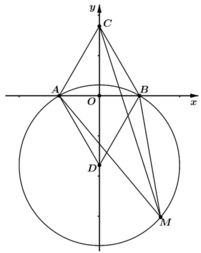
Chọn hệ trục Oxy sao cho Ox trùng với AB , chiều dương hướng từ A đến B ,trục Oy là đường trung trực của đoạn AB =>
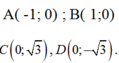
Phương trình đường tròn tâm D qua A; B là:
![]()
Giả sử M(a;b) là điểm bất kì trên đường tròn .Ta có :
MA2= (a+ 1) 2+ b2
MB2= (a-1) 2+ b2
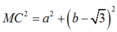

+ M nằm trên đường tròn (1) nên : 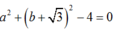
=> MA2+ MB2= MC2
=> MA; MB; MC là độ dài ba cạnh của một tam giác vuông.