Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng định nào sau đây sai?
A. S O ⊥ A B C D
B. C D ⊥ S B D
C. A B ⊥ S A C
D. C D ⊥ A C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 6 2023
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
28 tháng 12 2021
mình làm cũng hoang mang lắm bạn=), hay để hỏi cô xem sao
PT
1
CM
5 tháng 12 2018
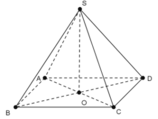
- Hình thoi ABCD có tâm O nên O là trung điểm AC và BD.
+) Tam giác SAC cân tại S( vì SA = SC) có SO là trung tuyến.
⇒ SO cũng là đường cao ⇒ SO ⊥ AC (1)
+) Tam giác SBD cân tại S( vì SB = SD) có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ BD (2)
- Từ (1), (2) suy ra S) ⊥ (ABCD).
+) Lại có: AB ⊂ mp(ABCD) nên SO ⊥ AB.
CM
11 tháng 7 2017
Dễ thấy BD ⊥ AC (tính chất hình thoi), BD ⊥ SC và BD ⊥ SA vì DB ⊥ (SAC).
Vì vậy phương án đúng là C.
16 tháng 2 2021
bị thừa nha bn tham khảo bn cần thì chép đến phần A thôi nha!
Đáp án B
+) Tam giác SAC cân tại S có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ AC.
+) Tam giác SBD cân tại S có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ BD.
- Từ đó suy ra SO ⊥ (ABCD).
→ Do ABCD là hình thoi nên CD không vuông góc với BD. Do đó CD không vuông góc với (SBD).