Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

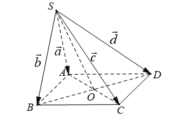
- Gọi O là tâm của hình bình hành ABCD. Ta có:
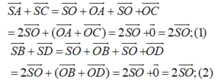
- Từ (1) và (2) suy ra:
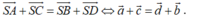

THAM KHẢO:

CD//AB nên góc giữa SB và CD là góc giữa AB và SB, \(\widehat{ABS}\)
CB//AD nên góc giữa SD và CB là góc giữa SD và AD, \(\widehat{ADS}\)
Ta có: tan\(\widehat{ABS}\)=tan\(\widehat{ADS}\)=\(\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
Suy ra \(\widehat{ABS}\)=\(\widehat{ADS}\)=\(\dfrac{\pi}{3}\)

Đáp án D
Tồn tại 5 mặt phẳng thỏa mãn đề bài là:
- Mp đi qua trung điểm AD,BC,SC,SD
- Mp đi qua trung điểm CD,AB,SC,SB
- Mp đi qua trung điểm AD,BC,SB,SA
- Mp đi qua trung điểm CD,AB,SA,SD
- Mp đi qua trung điểm SA,SB,SC,SD

mình làm cũng hoang mang lắm bạn=), hay để hỏi cô xem sao

a: Chọn mp(ABCD) có chứa CD
Xét ΔSBD có
E,I lần lượt là trung điểm của SB,SD
=>EI là đường trung bình của ΔSBD
=>EI//BD
Xét (ABCD) và (AIE) có
\(A\in\left(ABCD\right)\cap\left(AIE\right)\)
EI//BD
Do đó: (ABCD) giao (AIE)=xy, xy đi qua A và xy//BD//EI
Gọi K là giao điểm của xy với CD
=>K là giao điểm của CD với mp(AIE)
a: Chọn mp(ABCD) có chứa CD
Xét ΔSBD có
E,I lần lượt là trung điểm của SB,SD
=>EI là đường trung bình của ΔSBD
=>EI//BD
Xét (ABCD) và (AIE) có
EI//BD
Do đó: (ABCD) giao (AIE)=xy, xy đi qua A và xy//BD//EI
Gọi K là giao điểm của xy với CD
=>K là giao điểm của CD với mp(AIE)

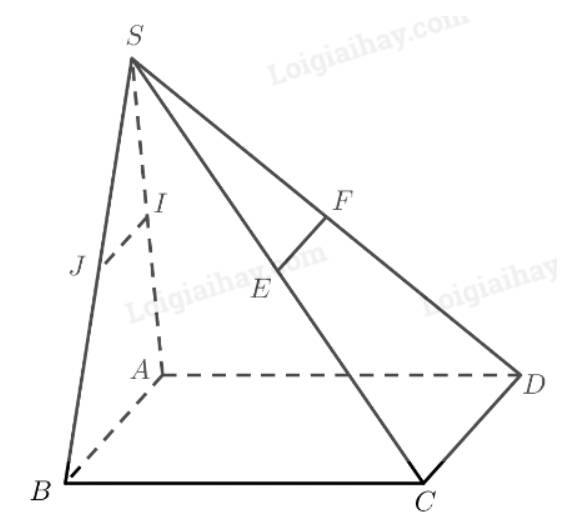
Ta có: \(I\) là trung điểm của \(SA\)
\(J\) là trung điểm của \(SB\)
\( \Rightarrow IJ\) là đường trung bình của tam giác \(SAB\)
\( \Rightarrow IJ\parallel AB\)
\(E\) là trung điểm của \(SC\)
\(F\) là trung điểm của \(SD\)
\( \Rightarrow EF\) là đường trung bình của tam giác \(SC{\rm{D}}\)
\( \Rightarrow EF\parallel C{\rm{D}}\)
Mà \(AB\parallel C{\rm{D}}\).
Vậy \(IJ\parallel EF\parallel AB\parallel C{\rm{D}}\).
Vậy \(AD\) không song song với \(IJ\)
Chọn C.

Kẻ \(BK\perp AC\Rightarrow BK\perp\left(SAC\right)\)
\(\Rightarrow BK=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow BK=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Kẻ \(CP\perp BH\Rightarrow CP\perp\left(SBH\right)\)
\(\Rightarrow CP=d\left(C;\left(SBH\right)\right)\)
\(\widehat{CBP}=\widehat{ACB}=30^0\Rightarrow CH=BC.sin30^0=\dfrac{a\sqrt{3}}{2}\)
\(BH=\dfrac{AC}{2}=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)\(\Rightarrow SH=\sqrt{SB^2-BH^2}=a\)
Kẻ \(HE\perp BC\) , kẻ \(HF\perp SE\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)
\(HE=CH.sin30^0=\dfrac{a}{2}\)
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{5}}{5}\)
Chọn A.
- Gọi O là tâm của hình bình hành ABCD. Ta có: