Vẽ hai góc kề bù x O y ^ và x O z ^ , biết x O y ^ = 130 0 .
a) Oy có nằm giữa hai tia Ox và Oz không?
b) Tính số đo của y O z ^
c) Vẽ tia Om là tia phân giác của x O y ^ , On là tia phân giác của y O z ^ . Chứng tỏ m O n ^ là góc vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/vì \(60^o< 130^o\)hay \(\widehat{xOy}< \widehat{xOz}\)
nên Oy nằm giữa 2 tia Ox à Oz
b/ta có: góc xOy+góc yOz=xOz
=>góc yOz=góc xOz-góc xOy=130o-60o=70o
vì 70o>60onên góc yOz>góc xOy
c/ta có Ox' là tia đối của Ox
=> góc xOx'=180o
=>góc xOz+góc zOx'=180o
=> góc zOx'=60o

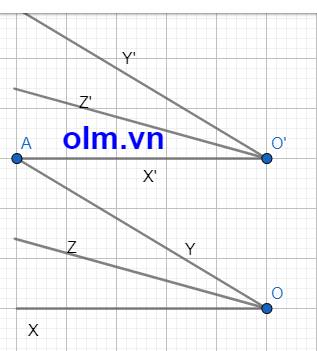
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
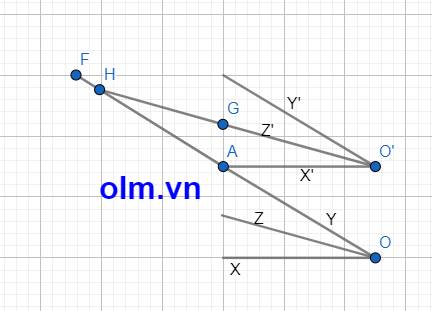
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)

Theo đề bài, ta có \widehat{nOz}=\frac{1}{2}\widehat{xOz},\widehat{mOz}=\frac{1}{2}\widehat{zOy}nOz=21xOz,mOz=21zOy.
Mặt khác, \widehat{xOz},\widehat{zOy}xOz,zOy là hai góc kề bù nên \widehat{xOz}+\widehat{zOy}=180^o.xOz+zOy=180o.
Do đó \widehat{nOm}=\widehat{nOz}+\widehat{mOz}=\frac{1}{2}\left(\widehat{xOz}+\widehat{yOz}\right)=90^onOm=nOz+mOz=21(xOz+yOz)=90o.