Tìm điều kiện của x để các phân thức sau xác định:
a) 2 x 2 x − 6 ; b) 1 x 2 − 4 x + 4 ;
c) x 27 x 3 + 27 x 2 + 9 x + 1 ; d) 5 4 x − 3 x 2 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



`a,x^3-8 ne 0`
`=>x^3 ne 8`
`=>x ne 2`
`b,2x^2+5x+3 ne 0`
`=>2x^2+2x+3x+3 ne 0`
`=>2x(x+1)+3(x+1) ne 0`
`=>(x+1)(2x+3) ne 0`
`=>x ne -1,-3/2`
`c,x^2-4 ne 0`
`=>x^2 ne 4`
`=>x ne 2,-2`
a) ĐK:
\(x^3-8\ne0\\ \Leftrightarrow x\ne2\)
b) ĐK:
\(2x^2+5x+3\ne0\\ \Leftrightarrow\left[{}\begin{matrix}x\ne-1\\x\ne-\dfrac{3}{2}\end{matrix}\right.\)
c) ĐK:
\(x^2-4\ne0\\ \Leftrightarrow x\ne\pm2\)

a: ĐKXĐ: \(x\notin\left\{\dfrac{5}{2};-\dfrac{5}{2}\right\}\)

Lời giải:
a. Để biểu thức xác định thì:
$x^2-x-6\geq 0$
$\Leftrightarrow (x+2)(x-3)\geq 0$
$\Leftrightarrow x\geq 3$ hoặc $x\leq -2$
b. Để biểu thức xác định thì:
$4x-x^2-5\geq 0$
$\Leftrightarrow x^2-4x+5\leq 0$
$\Leftrightarrow (x-2)^2+1\leq 0$
$\Leftrightarrow (x-2)^2\leq -1< 0$ (vô lý)
Vậy không tồn tại $x$ để bt xác định
c. Để biểu thức xác định thì:
$x^2-8x+15>0$
$\Leftrightarrow (x-3)(x-5)>0$
$\Leftrightarrow x>5$ hoặc $x< 3$
a) ĐKXĐ: \(\left[{}\begin{matrix}x\ge3\\x\le-2\end{matrix}\right.\)
b) ĐKXĐ: \(x\in\varnothing\)
c) ĐKXĐ: \(\left[{}\begin{matrix}x>5\\x< 3\end{matrix}\right.\)

\(a,\sqrt{2x-5}\)
Biểu thức trên xác định \(\Leftrightarrow2x-5\ge0\)
\(\Leftrightarrow2x\ge5\)
\(\Leftrightarrow x\ge\dfrac{5}{2}\)
\(b,\sqrt{3x+1}\)
Biểu thức trên xác định \(\Leftrightarrow3x+1\ge0\)
\(\Leftrightarrow3x\ge-1\)
\(\Leftrightarrow x\ge-\dfrac{1}{3}\)
\(c,\dfrac{2}{x+2}\)
Biểu thức trên xác định \(\Leftrightarrow x+2\ne0\)
\(\Leftrightarrow x\ne-2\)

Câu 5: B
Câu 6:
a: ĐKXĐ: \(x-2\ne0\)
=>\(x\ne2\)
b: ĐKXĐ: \(x+1\ne0\)
=>\(x\ne-1\)
8:
\(A=\dfrac{x^2+4}{3x^2-6x}+\dfrac{5x+2}{3x}-\dfrac{4x}{3x^2-6x}\)
\(=\dfrac{x^2+4-4x}{3x\left(x-2\right)}+\dfrac{5x+2}{3x}\)
\(=\dfrac{\left(x-2\right)^2}{3x\left(x-2\right)}+\dfrac{5x+2}{3x}\)
\(=\dfrac{x-2+5x+2}{3x}=\dfrac{6x}{3x}=2\)
7:
\(\dfrac{8x^3yz}{24xy^2}\)
\(=\dfrac{8xy\cdot x^2z}{8xy\cdot3y}\)
\(=\dfrac{x^2z}{3y}\)

1) \(\dfrac{5-x}{x^2-3x}=\dfrac{5-x}{x\left(x-3\right)}\left(đk:x\ne0,x\ne3\right)\)
2) \(\dfrac{3x}{2x+3}\left(đk:x\ne-\dfrac{3}{2}\right)\)

Để phân thức xác định:
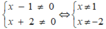
Vậy điều kiện để phân thức xác định là x ≠ -2 và x ≠ 1

đk để xác định: \(x^2+1\ne0\)
=>x là số nào cũng được vì \(x^2+1\) luôn luôn > 0
A=1/(x^2+1)
A xác định khi x^2+1 khác 0
mà x^2+1 lớn hơn 0 với mọi x
suy ra A xác định với mọi GT của x