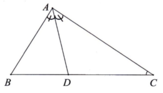
Cho tam giác ABC, tia phân giác AD (D thuộc BC). Tính A D B ^ và A D C ^ biết B ^ − C ^ = 40 ° .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


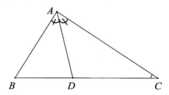

A A B B C C D 1 1 1 2
Xét \(\Delta ABC\) có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\)\(\widehat{B}+\widehat{C}=180^0-\widehat{A}\)
Do đó :
\(\widehat{B}=\frac{180^0-\widehat{A}+40^0}{2}=\frac{220^0-\widehat{A}}{2}=\frac{220^0-2\widehat{A}_1}{2}=110^0-\widehat{A_1}\)
Xét \(\Delta ADB\) có :
\(\widehat{A_1}+\widehat{B}+\widehat{ADB}=180^0\)
\(\Rightarrow\)\(\widehat{A_1}+110^0-\widehat{A_1}+\widehat{ADB}=180^0\)
\(\Rightarrow\)\(\widehat{ADB}=70^0\)
Mà \(\widehat{ADB}+\widehat{ADC}=180^0\) ( hai góc kề bù )
\(\Rightarrow\)\(70^0+\widehat{ADC}=180^0\)
\(\Rightarrow\)\(\widehat{ADC}=110^0\)
Vậy \(\widehat{ADB}=70^0\) và \(\widehat{ADC}=110^0\)
Chúc bạn học tốt ~

Tam giác ABC vuông tại A
=>góc BAC=90°
AD là tia phân giác của tam giác ABC
=>góc BAD=góc CAD=góc BAC/2=45°
Ta lại có,tam giác CAH vuông tại H( vì AH_|_BC theo gt)
=> góc AHC=90°
Xét tam giác vuông ACH,có:
góc HAC =180°-(góc AHC+góc ACH)
=180°-(90°+40°)=50°
=>góc HAD=góc HAC-góc DAC
=50°-45°
=5°
Ta có
tam giác AHC có
HAC+ AHC+HCA=180 nên HAC=180-AHC-HCA=180-90-40=50
Tam giác DAC có BAD=DAC=45( AD là tia phân giác)
Mà HAD+DAC=HAC nên HAD=5

tính p = (a+b+c)/2
AD=2/(b+c)* caăn (p*b*c*(p-a))