

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 1:
a: XétΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD
b: Xét ΔDBC và ΔECB có
DB=EC
BC chung
DC=EB
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{KDB}=\widehat{KEC}\)
Xét ΔKDB và ΔKEC có
\(\widehat{KDB}=\widehat{KEC}\)
BD=CE
\(\widehat{KBD}=\widehat{KCE}\)
Do đó: ΔKDB=ΔKEC


a, Xét tam giác ADB và tam giác ADC có
AD _ chung ; ^DAB = ^DAC ; AB = AC
Vậy tam giác ADB = tam giác ADC (c.g.c)
b, Xét tam giác ABC cân tại A có AD là phân giác
đồng thời là đường cao hay AD vuông BC
c, Xét tam giác AMD và tam giác AND có
AD _ chung ; ^MAD = ^NAD
Vậy tam giác AMD = tam giác AND ( ch-gn )
=> AM = AN ( 2 cạnh tương ứng )
d, Ta có AM/AB = AN/AC => MN // BC ( Ta lét đảo )

Bạn tự vẽ hình nhé![]()
a) góc B + C + A =180*
suy ra : 70* + 50* +A =180*
suy ra : góc A = 180 -70 -50 = 60*
vì AD là tia p/giác suy ra: BAD = DAC = 60* /2= 30*
BAD + B + ADB = 180*
suy ra: 30+ 70+ADB =180
suy ra : ADB = 180 -(30+70)=80*
Do AH vuông BC suy ra AHD=90*
BDA + ADH =180*(2góc kề bù)
suy ra :80* +ADH =180*
suy ra : ADH = 100*
ADH +AHD + HAD = 180*
suy ra : 100 + 90 + HAD =180
suy ra : HAD =? SAI ĐỀ RÙI HAY SAO Ý![]()
![]()
![]()

a)Xét ΔAMD và ΔCMB có :
góc AMB = góc CMD ( đối đỉnh)
AM = NC ( GT)
BM = MD ( GT)
--->ΔAMD = ΔCMB(c.g.c)
b) ta có góc CAD = góc ACB(ΔAMD = ΔCMB)
tạo ra hai góc so le trong bằng nhau
--->AD//BC
c)Xét ΔABC và ΔCDA có :
AC : cạnh chung
AD = BC (ΔAMD = ΔCMB)
góc CAD = góc ACB(ΔAMD = ΔCMB)
--->ΔABC = ΔCDA(c.g.c)
d)ta có AE + ED = AD
AF+ FC = BC
mà EF= BF; AD = BC
--->AE = FC
xét ΔAFC và ΔACE có :
AE = FC (CMT)
AC : cạnh chung
góc CAE = góc ACF (ΔAMD = ΔCMB)
--->ΔAFC = ΔCEA ( c.g.c)
--->góc AEC = góc AFC ( hai góc tương ứng)
--->góc AEC = góc AFC=90'
--->AF vuông góc với BC

a) Xét t/g AMD và t/g CMB có:
AM = CM (gt)
AMD = CMB ( đối đỉnh)
MD = MB (gt)
Do đó, t/g AMD = t/g CMB (c.g.c) (đpcm)
b) t/g AMD = t/g CMB (câu a)
=> ADM = CBM (2 góc tương ứng)
Mà ADM và CBM là 2 góc so le trong nên AD // BC (đpcm)
c) t/g AMD = t/g CMB (câu a)
=> AD = BC (2 cạnh tương ứng)
Xét t/g ABC và t/g CDA có:
BC = AD (gt)
ACB = CAD (so le trong)
AC là cạnh chung
Do đó, t/g ABC = t/g CDA (c.g.c) (đpcm)
d) Có: AD = BC (câu c)
DE = BF (gt)
Suy ra AD - DE = BC - BF
=> AE = CF
Mà AE // CF do AD // BC (câu b)
Nên CE // AF ( vì theo tính chất đoạn chắn AE = CF khi AE // CF và CE // AF)
Lại có: CE _|_ AD (gt) => AF _|_ AD
Mà BC // AD (câu b) => AF _|_ BC (đpcm)

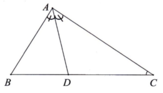
Bài 2:
\(\widehat{ADB}=180^0-80^0=100^0\)
Ta có: \(\widehat{ADB}+\widehat{BAD}+\widehat{B}=\widehat{ADC}+\widehat{CAD}+\widehat{C}\)
\(\Leftrightarrow\widehat{B}+100^0=\widehat{C}+80^0\)
\(\Leftrightarrow1.5\widehat{C}-\widehat{C}=-20^0\)
\(\Leftrightarrow\widehat{C}=40^0\)
hay \(\widehat{B}=60^0\)
=>\(\widehat{BAC}=80^0\)