Cho biết 3cosα – sinα = 1; 00 < α < 900. Giá trị của tanα bằng:
A. 4/3
B. 3/4
C. 1
D. ½
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 3 cos α − sin α = 1 ⇔ 3 cos α = sin α + 1 → 9 cos 2 α = sin α + 1 2
⇔ 9 cos 2 α = sin 2 α + 2 sin α + 1 ⇔ 9 1 − sin 2 α = sin 2 α + 2 sin α + 1
⇔ 10 sin 2 α + 2 sin α − 8 = 0 ⇔ sin α = − 1 sin α = 4 5 .
sin α = − 1 : không thỏa mãn vì 0 0 < α < 90 0 .
sin α = 4 5 ⇒ cos α = 3 5 ⇒ tan α = sin α cos α = 4 3 .
Chọn A.

Ta có:
3 cos α − sin α = 1 ⇔ 3 cos α = sin α + 1 → 9 cos 2 α = sin α + 1 2
⇔ 9 cos 2 α = sin 2 α + 2 sin α + 1 ⇔ 9 1 − sin 2 α = sin 2 α + 2 sin α + 1
⇔ 10 sin 2 α + 2 sin α − 8 = 0 ⇔ sin α = − 1 sin α = 4 5 .
sin α = − 1 : không thỏa mãn vì 0 0 < α < 90 0 .
sin α = 4 5 ⇒ cos α = 3 5 ⇒ tan α = sin α cos α = 4 3 .
Chọn A.

Chọn A.
Ta có 3cosα+ 2sinα = 2 hay (3cosα+ 2sinα = 2 )2 = 4
Tương đương: 9 cos2 α + 12 cosα .sin α + 4sin2α = 4
Hay 5cos2α + 12 cosα .sin α = 0
Từ đó: cosα= 0 hoặc 5cosα + 12 sinα = 0
+ Nếu cosα = 0 thì sinα =1: loại ( vì sinα < 0).
+ 5cosα + 12 sinα = 0
ta có hệ phương trình 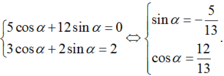

a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3

Bài 1:
\(\cos\alpha=\sqrt{1-\dfrac{9}{25}}=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{3}{5}:\dfrac{4}{5}=\dfrac{3}{4}\)
Bài 2:
\(\sin\alpha=\sqrt{1-\dfrac{49}{100}}=\dfrac{\sqrt{51}}{10}\)
\(\tan\alpha=\dfrac{\sqrt{51}}{7}\)

Lời giải:
Áp dụng BĐT Bunhiacopxky:
$P^2=(2\sin a+3\cos a)^2\leq (2^2+3^2)(\sin ^2a+\cos ^2a)=13$
$\Rightarrow P\leq \sqrt{13}$
Vậy $P_{\max}=\sqrt{13}$
Giá trị này đạt tại $\frac{\sin a}{2}=\frac{\cos a}{3}$

Bài 3:
Ta có: \(A=\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)
\(=\left(\sin^270^0+\cos^270^0\right)+\left(\sin^250^0+\cos^250^0\right)\)
=1+1
=2

\(a,VT=cot\alpha+\dfrac{sin\alpha}{1+cos\alpha}\\ =\dfrac{cos\alpha}{sin\alpha}+\dfrac{sin\alpha}{1+cos\alpha}\\ =\dfrac{cos\alpha\left(1+cos\alpha\right)+sin^2\alpha}{sin\alpha\left(1+cos\alpha\right)}\\ =\dfrac{cos\alpha+cos^2\alpha+sin^2\alpha}{sin\alpha\left(1+cos\alpha\right)}\\ =\dfrac{cos\alpha+1}{sin\alpha\left(1+cos\alpha\right)}\\ =\dfrac{1}{sin\alpha}=VP\left(dpcm\right)\)
\(b,VT=\dfrac{1}{1-sin\alpha}+\dfrac{1}{1+sin\alpha}\\ =\dfrac{1+sin\alpha+1-sin\alpha}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}\\ =\dfrac{2}{1-sin^2\alpha}\\ =\dfrac{2}{cos^2\alpha}=VP\left(dpcm\right)\)
Chọn A.
Ta có 3cosα – sinα = 1 nên 3cosα = sinα + 1
Suy ra: 9cos2α = sin2α + 2sinα + 1
Hay 10sin2α + 2sinα - 8 = 0
Do đó: sinα = -1 hoặc sinα = 0,8
+ sinα = -1 không thỏa mãn vì 00 < α < 900
+ sinα = 0,8 thì cosα = 0,6 và tan α = 0,8 : 0,6 = 4/3.