
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì tan α = 2 nên cos α ≠ 0
Ta có: G = 2 sin α + cos α cos α − 3 sin α = 2 sin α cos α + cos α sin α cos α cos α − 3 sin α cos α = 2 tan α + 1 1 − 3 tan α
Thay tan α = 2 ta được: G = 2.2 + 1 1 − 3.2 = − 5 5 = − 1
Vậy G = −1
Đáp án cần chọn là: D

Đặt \(A=sin\alpha+sin\left(90^0-\alpha\right)=sin\alpha+cos\alpha\)
\(\Rightarrow A^2=\left(sin\alpha+cos\alpha\right)^2\le2\left(sin^2\alpha+cos^2\alpha\right)=2\)
\(\Rightarrow A\le\sqrt{2}\)
\(A_{max}=\sqrt{2}\) khi \(\alpha=45^0\)

S A B C = . AB. AC ≤ 1 2 . A B 2 + A C 2 2 = 1 4 . A B 2 + A C 2
Áp dụng định lý Py-ta-go cho ABC vuông tại A ta có:
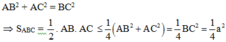
Dấu “=” xảy ra AC = AB => ∆ ABC vuông cân
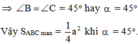
Đáp án cần chọn là: D

\(A=\dfrac{\dfrac{3sina}{cosa}-\dfrac{5cosa}{cosa}}{\dfrac{5sina}{cosa}+\dfrac{8cosa}{cosa}}=\dfrac{3tana-5}{5tana+8}=\dfrac{3.\left(\dfrac{5}{7}\right)-5}{5.\left(\dfrac{5}{7}\right)+8}=...\)

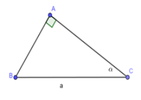
Dựng tam giác vuông có cạnh huyền bằng 3, một cạnh góc vuông có độ dài bằng 2, khi đó góc kề cạnh góc vuông có độ dài bằng 2 là góc α cần dựng
Ta có: cosα = 2 3 => α ≈ 48 0 11 '

\(=\sqrt{3}\left(\sqrt{3}sina+cosa\right)\)
\(=\sqrt{3}\cdot2\left(\frac{\sqrt{3}}{2}sina+\frac{1}{2}cosa\right)\)
\(=2\sqrt{3}\left(cos30sina+sin30cosa\right)\)
\(=2\sqrt{3}sin\left(a+30\right)\)
Ta có \(-1\le sin\left(a+30\right)\le1\)
\(-2\sqrt{3}\le2\sqrt{3}sin\left(a+30\right)\le2\sqrt{3}\)
P đạt GTLN
\(\Leftrightarrow2\sqrt{3}sin\left(a+30\right)=2\sqrt{3}\)
\(sin\left(a+30\right)=1\)
\(a+30=90+k360\) ( vì a góc nhọn nên bỏ k 360 độ đi )
\(a+30=90\)
\(a=60\)
Vậy P dạt GTLN là \(2\sqrt{3}\) \(\Leftrightarrow a=60\)

Lời giải:
Áp dụng công thức $\sin ^2a+\cos ^2a=1$ và BĐT Bunhiacopxky:
$(\sin a+\cos a)^2\leq (\sin ^2a+\cos ^2a)(1+1)=2$
$\Rightarrow \sin a+\cos a\leq \sqrt{2}$
Vậy GTLN của $\sin a+\cos a$ là $\sqrt{2}$

Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay vào P ta được
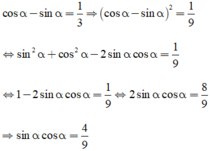
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$P^2=(2\sin a+3\cos a)^2\leq (2^2+3^2)(\sin ^2a+\cos ^2a)=13$
$\Rightarrow P\leq \sqrt{13}$
Vậy $P_{\max}=\sqrt{13}$
Giá trị này đạt tại $\frac{\sin a}{2}=\frac{\cos a}{3}$
Em cảm ơn ạ