Hàm số y = ln ( x 2 − 2 x + m ) có tập xác định là R khi:
A. m > 1
B. m ≥ 1
C. m > 0
D. m ≥ 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 8 2018
Đáp án: D.
y' = 3 x 2 - 6(m - 1)x - 3(m + 1)
y' = 0 ⇔ x 2 - 2(m - 1)x - m - 1 = 0
Δ' = ( m - 1 ) 2 + m + 1 = m 2 - m + 2 ≥ 0
Tam thức m 2 - m + 2 luôn dương với mọi m ∈ R vì δ = 1 - 8 < 0 và a = 1 > 0 cho nên phương y' = 0 luôn có hai nghiệm phân biệt. Suy ra hàm số luôn có cực trị với mọi giá trị m ∈ R.
CM
8 tháng 6 2017
Đáp án: D.
y' = 3 x 2 - 6(m - 1)x - 3(m + 1)
y' = 0 ⇔ x 2 - 2(m - 1)x - m - 1 = 0
∆ ' = m - 1 2 + m + 1 = m 2 - m + 2 ≥ 0
Tam thức m 2 - m + 2 luôn dương với mọi m ∈ R vì δ = 1 - 8 < 0 và a = 1 > 0 cho nên phương y' = 0 luôn có hai nghiệm phân biệt. Suy ra hàm số luôn có cực trị với mọi giá trị m ∈ R.
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2021
a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)
CM
8 tháng 2 2019
Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
Δ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 
CM
13 tháng 7 2019
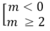
Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
∆ ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 
CM
2 tháng 9 2018
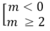
Đáp án: B.
Hàm số đã cho có cực trị khi và chỉ khi
y' = 3 x 2 - 6(m - 1)x - 3(m + 3) = 0 có 2 nghiệm phân biệt
⇔ ∆ ' = m - 1 2 + (m + 3) = m 2 - m + 4 > 0
Ta thấy tam thức ∆ ' = m 2 - m + 4 luôn dương với mọi m vì
δ = 1 - 16 = -15 < 0, a = 1 > 0
Vậy hàm số đã cho luôn có cực trị mới mọi m ∈ R
CM
6 tháng 8 2019
Đáp án: B.
Hàm số đã cho có cực trị khi và chỉ khi
y' = 3 x 2 - 6(m - 1)x - 3(m + 3) = 0 có 2 nghiệm phân biệt
⇔ Δ' = ( m - 1 ) 2 + (m + 3) = m 2 - m + 4 > 0
Ta thấy tam thức Δ' = m 2 - m + 4 luôn dương với mọi m vì
δ = 1 - 16 = -15 < 0, a = 1 > 0
Vậy hàm số đã cho luôn có cực trị mới mọi m ∈ R
Đáp án A.
Hàm số xác định trên ℝ ⇒ x 2 − 2 x + m > 0 ∀ x ∈ ℝ
⇔ Δ ' < 0 a > 0 ⇔ 1 2 − m < 0 1 > 0 ⇔ m > 1