Cho hình thang cân ABCD có đáy nhỏ AB. Biết AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất của hình thang.
A. 8 2 9
B. 4 2 9
C. 3 3 2
D. 3 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
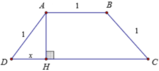
Dựng A H ⊥ C D . Đặt D H = x 0 < x < 1
Ta có: D C = 2 x + 1 ⇒ A H = 1 − x 2
S A B C D = 1 + 2 x + 1 2 1 − x 2 = 1 + x 1 − x 2 = f x ⇒ f ' x = 1 − x 2 − 1 + x x 1 − x 2 = 0 ⇔ 1 − x 2 = 1 + x x ⇔ 2 x 2 + x − 1 = 0 ⇔ x = − 1 l o a i x = 1 2 ⇒ S m a x = f 1 2 = 3 3 4 ⇔ x = 1 2
Đáp án D
Kẻ AM vuông góc với CD tại M.
Đặt D M = a . Ta có A M = 1 − a 2 ; C D = 2 a + 1
Diện tích của hình thang là
S = 1 2 A B + C D . A M = 1 2 2 a + 2 1 − a 2 = a + 1 1 − a 2
Bài toán trở thành tìm giá trị lớn nhất của hàm số f a = a + 1 1 − a 2 trên (0;1)
Sử dụng chức năng TABLE của máy tính ta nhập
Nhìn vào bảng giá trị ta thấy giá trị lớn nhất của hàm số ≈ 1,299 . So sánh với các phương án chỉ thấy D thỏa mãn, ta chọn D.