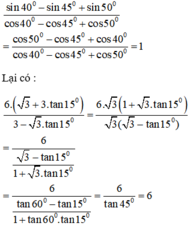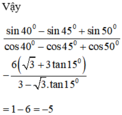Không sử dụng máy tính, hãy chứng minh:
K
Khách
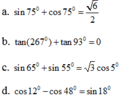
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
26 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
21 tháng 10 2021
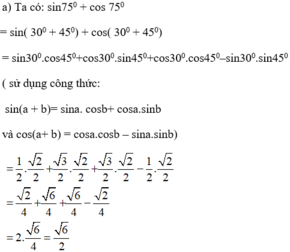
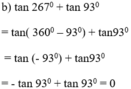
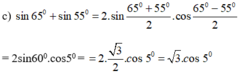
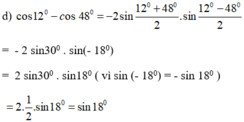
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
PT
1
NL
7
16 tháng 9 2017
Một cách khác nhé!
Đặt a=2014, b=2015 => b-a=1
Khi đó: \(Q=\sqrt{a^2+a^2b^2+b^2}=\sqrt{\left(b-a\right)^2+a^2b^2+2ab}=\sqrt{a^2b^2+2ab+1}=\sqrt{\left(ab+1\right)^2}\)
\(=ab+1=2014.2015+1=4058211\)
15 tháng 9 2017
Đặt \(2014=a\) thì ta có:
\(Q=\sqrt{a^2+a^2.\left(a+1\right)^2+\left(a+1\right)^2}\)
\(=\sqrt{a^4+2a^3+3a^2+2a+1}\)
\(=\sqrt{\left(a^2+a+1\right)^2}=a^2+a+1\)
Vậy Q là số nguyên
CM
20 tháng 6 2018
Ta có: sin 40º = cos 50º ; sin 45º = cos 45º ; sin 50º = cos 40º
Do đó :
KL
0