Cho các số phức khác không, thỏa mãn z 1 2 - z 1 . z 2 + z 2 2 = 0 . Gọi A, B là các điểm biểu diễn tương ứng của z 1 , z 2 Khi đó tam giác OAB là tam giác
A. Đều
B. vuông tại O
C. Tù
D. vuông tại A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+0}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2\left(x+y+z\right)}{xyz}}\)
\(=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2}{xy}+\dfrac{2}{yz}+\dfrac{2}{zx}}=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}\)
\(=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\) là số hữu tỉ

Đáp án D.
Đặt z = a + bi => a + bi ![]()
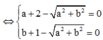
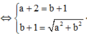
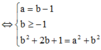

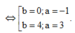
Do |z| > 1 => a = 3, b = 4
Đáp án A.