Cho hình nón có thiết diện qua trục là một tam giác đều. Khai triển hình nón theo một đường sinh, ta được một hình quạt tròn có góc ở tâm là α . Trong các kết luận sau, kết luận nào là đúng?
A. α = 2 π 3
B. α = π 2
C. α = π
D. α = 3 π 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

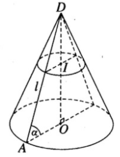
Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’
với 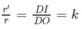
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:
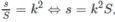
trong đó S = πr 2 = πl 2 cos 2 α
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: s = k 2 s = k 2 πl 2 cos 2 α

Đáp án D
Δ S A B vuông cân tại S , A B = 4 a
⇒ S A = S B = 4 a 2 = 2 a 2
⇒ l = 2 a 2
Δ S A C cân tại S , A S C ^ = 120 0
⇒ S A C ^ = S C A ^ = 30 0
⇒ c o s S A O ^ = O A S A hay 3 2 = R 2 a 2 ⇒ R = a 6
S x q = π R l = π . a 6 .2 a 2 = π 4 a 2 3 .

Đáp án C
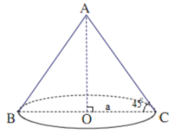
Giả sử thiết diện qua trục hình nón là DABC như hình vẽ. Vì DABC cân tại A, góc ở đáy bằng 45 ° nên DABC vuông cân tại A. Gọi O là tâm của đáy ⇒ O A = O B = O C = a , vậy O là tâm mặt cầu ngoại tiếp hình nón, bán kính bằng a → thể tích mặt cầu bằng: 4 3 π a 3
Đáp án C
Gọi hình nón có bán kính đáy là r => Độ dài đường sinh l = 2 r . Khi đó, khi khai triển hình nón theo đường sinh ta được hình quạt có bán kính R = l = 2 r và độ dài cung tròn L = C = 2 π r .
Mặt khác L = α R ⇒ α = 2 π r 2 r = π .