Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r = và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl = ( đơn vị diện tích)
Sđáy = =
( đơn vị diện tích);
Vnón =
( đơn vị thể tích)
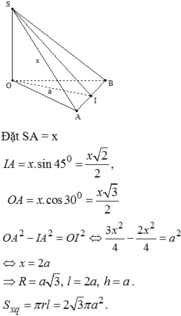
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết, = 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 = .
Vậy .
Ta có ∆ OIB vuông ở I và BO = r = ;
OI = SI.cos600 = .
Vậy BI = và BC =
.
Do đó S = (SI.BC)/2 = (đơn vị diện tích)

Phương pháp:
Xác định góc giữa hai mặt phẳng và tính toán dựa vào các kiến thức hình học đã biết.
Cách giải:
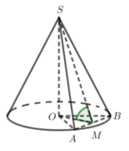


Phương pháp:
+) Gọi S là đỉnh hình nón và O là tâm đường tròn đáy của hình nón. Giả sử (P) cắt nón theo thiết diện là tam giác SAB.
+) Gọi M là trung điểm của AB, tính SM, từ đó tính S S A B
Cách giải:
Gọi S là đỉnh hình nón và O là tâm đường tròn đáy của hình nón.
Giả sử (P) cắt nón theo thiết diện là tam giác SAB.
Gọi M là trung điểm của AB ta có
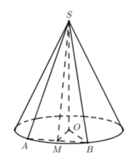


Đáp án D
Δ S A B vuông cân tại S , A B = 4 a
⇒ S A = S B = 4 a 2 = 2 a 2
⇒ l = 2 a 2
Δ S A C cân tại S , A S C ^ = 120 0
⇒ S A C ^ = S C A ^ = 30 0
⇒ c o s S A O ^ = O A S A hay 3 2 = R 2 a 2 ⇒ R = a 6
S x q = π R l = π . a 6 .2 a 2 = π 4 a 2 3 .

Đáp án C.
Phương pháp:
Diện tích xung quanh của hình nón: S x q = π R l
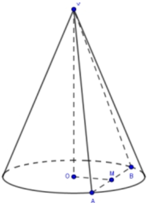
Cách giải:
Gọi M là trung điểm AB ⇒ O M ⊥ A B . Mà O M ⊥ S O (vì SO vuông góc với đáy)
⇒ OM là đoạn vuông góc chung của SO và AB
⇒ d S O ; A B = O M = 3
Tam giác OMA vuông tại M:
O A 2 = O M 2 + M A 2 ⇒ R 2 = 3 2 + M A 2 ⇒ M A = R 2 − 9
Tam giác SAB vuông tại A có S A = S B (Vì Δ S O B = Δ S O A c . g . c )
⇒ Δ S A B vuông cân tại S
⇒ S A = A B 2 = 2 A M 2 = A M . 2 = 3 R 2 − 18
(N) có góc ở đỉnh là
120 0 ⇒ A S O = 60 0
Tam giác SOA vuông tại O:
sin O S A = O A S A ⇒ sin 60 0 = R 3 R 2 − 18 = 3 2 ⇒ 2 R = 3 . 3 R 2 − 18 ⇔ 4 R 2 = 6 R 2 − 54
⇔ R 2 = 27 ⇒ R = 3 3 .
l = S A = 2 R 2 − 18 = 2.27 − 18 = 36 = 6
S x q = π R l = π .3 3 .6 = 18 π 3



Chọn C