Cho a > 0 , b > 0 thỏa mãn a 2 + 4 b 2 = 5 a b . Khẳng định nào sau đây đúng?
A. 2 log a + 2 b = 5 log a + log b
B. log a + 1 + log b = 1
C. log a + 2 b 3 = log a + log b 2
D. 5 log a + 2 b = log a - log b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D
Cho 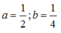 ta thấy logab= 2 và logba= ½. Do vậy logba< 1< logab
ta thấy logab= 2 và logba= ½. Do vậy logba< 1< logab

Đáp án B
a 2 + 9 b 2 = 10 a b ⇔ a + 3 b 2 = 16 a b ⇔ a + 3 b 4 = a b ⇒ log a + 3 b 4 = log a + log b 2

Đáp án C
Ta có log a b < 0 ⇔ log a b < log a 1. Xét 2 trường hợp
T H 1 : a > 1 suy ra log a b < log a 1 ⇔ b < 1. Kết hợp điều kiện ta được 0 < b < 1 < a
T H 2 : 0 < a < 1 suy ra log a b < log a 1 ⇔ b > 1. Kết hợp điều kiện ta được 0 < a < 1 < b
Vậy khẳng định đúng là 0 < a < 1 < b 0 < b < 1 < a