Trong không gian Oxyz. Cho tứ diện đều ABCD có A(0;1;2) và hình chiếu vuông góc của A trên mặt phẳng (BCD) là H (4; -3;-2). Tọa độ tâm I của mặt cầu ngoại tiếp tứ diện ABCD.
A. I(3; -2;-1).
B. I(2;-1;0).
C. I(3; -2;1).
D. I(-3; -2;1).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 1 2018
Đúng(0)
Những câu hỏi liên quan
CM
31 tháng 3 2017
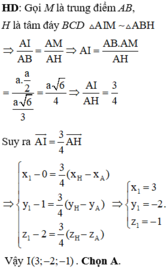
Đáp án C
Do ABCD là tứ diện đều nên H là trọng tâm tam giác BCD và I trùng với trọng tâm G của tứ diện ABCD. Ta có:
Từ đó ta có:
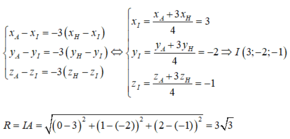
Vậy đáp án C đúng.
CM
25 tháng 3 2018
Chọn đáp án C.
Ta có
Áp dụng công thức ta có:
V A B C D = 1 6 A B ⇀ . A C ⇀ . A D ⇀ = 1 2
CM
30 tháng 9 2018
Đáp án C
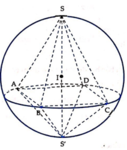
Mặt cầu (S) có tâm I 1 ; 0 ; 2 , bán kính R=3. Nhận xét thấy S, I, S’ thẳng hàng và S S ' ⊥ A B C D . Khi đó S S ' = 2 R = 6 . Ta có:
V H = V S . A B C D + V S ' . A B C D = 1 3 d S ; A B C D . S A B C D + 1 3 d S ' ; A B C D . S A B C D
= 1 3 d S ; A B C D + d S ' ; A B C D . S A B C D = 1 3 S S ' . S A B C D = 2 S A B C D
Từ giả thiết suy ra ABCD là hình vuông, gọi a là cạnh hình vuông đó.
Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng r và ngoại tiếp hình vuông ABCD.
Suy ra 2 r = A C = a 2 ⇒ r = a 2 2 . Từ d I ; P 2 + r 2 = R 2 .
⇔ r = R 2 − d I ; P 2 = 3 2 − 8 3 2 = 17 3 = a 2 2 ⇔ a = 2 17 3 2
Vậy V H = 2 S A B C D = 2 a 2 = 2. 2 17 3 2 2 = 68 9 .
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1 2022
Không có mặt phẳng nào là mặt phẳng Oxyz cả nên chắc đề ko đúng. Giả sử nó là Oxy đi
Ý tưởng giải bài toán như sau:
- Viết phương trình mp trung trực (P) của đoạn AB
- Viết pt tham số đường thẳng d là giao của (P) và Oxy
- C thuộc d nên quy tọa độ C về 1 ẩn
- Tính độ dài AB=AC sẽ tìm được tọa độ C
- Viết phương trình mp trung trực (Q) của AC
- Viết pt tham số đường thẳng d1 là giao của (P) và (Q)
- D thuộc d1 => quy tọa độ D theo 1 ẩn, tính độ dài AD=AB => tọa độ D
Câu b thì giải hệ 3 tích vô hướng: SA.SB, SA.SC, SB.SC=0