Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A

Phương pháp:
Cách giải:


Mà AH vuông góc (BCD) nên AH là trục của mặt phẳng (BCD).
Gọi K là trung điểm AD, kẻ OK vuông góc với AD, O thuộc AH


Chọn A
Coi như a =1. Tam giác ACD vuông tại A nên A D = C D 2 - A C 2 = 1 = A B ⇒ Δ A B D cân tại A và tam giác ACD vuông cân tại A. Gọi H, E lần lượt là trung điểm của BD và DC. Ta có A H ⊥ ( B C D ) và C D ⊥ A E . Hơn nữa C D ⊥ A H ⇒ C D ⊥ ( A H E ) ⇒ C D ⊥ H E mà HE song song với BC suy ra BC vuông góc với CD. H là tâm của đường tròn ngoại tiếp tam giác BCD, do đó AH là trục đường tròn này. Trong tam giác AHE dựng đường thẳng qua E vuông góc AE và cắt AH tại điểm I. Do mặt phẳng (AHE) vuông góc với mặt phẳng (ACD) nên d cũng vuông góc với (ACD). Hơn nửa E là tâm của đường tròn ngoại tiếp tam giác ACD suy ra I là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Ta có A I . A H = A E 2 ⇒ A I = A E 2 A H . Ta có
A E = 1 2 C D = 2 2 , H K = 1 2 B C = 1 2 ⇒ A H = 1 2
Vậy A I = A E 2 A H = 1 ⇒ R = 1 ⇒ V m c = 4 3 π

Chọn D.
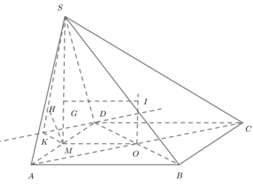
Phương pháp: Xác định cạnh của đáy trước.
Cách giải: Bán kính mặt cầu ngoại tiếp khối chóp là ![]()
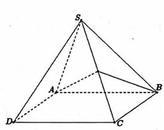
Gọi O là tâm của đáy, I là tâm mặt cầu, G là tâm tam giác SAD, M là trung điểm AD.
Dễ thấy I nằm đồn thời trên trục của tam giác SAD và trục của đáy.
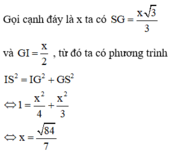
Qua D dựng đường thẳng d song song với AC. Gọi K là hình chiếu cửa M trên d, H là hình chiếu của M trên SD. Suy ra M H ⊥ d , S D .
Ta có:
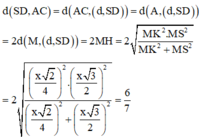
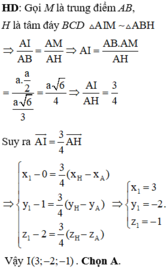

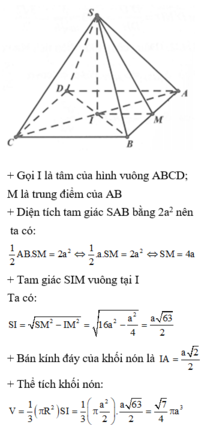




Đáp án C
Mặt cầu (S) có tâm I 1 ; 0 ; 2 , bán kính R=3. Nhận xét thấy S, I, S’ thẳng hàng và S S ' ⊥ A B C D . Khi đó S S ' = 2 R = 6 . Ta có:
V H = V S . A B C D + V S ' . A B C D = 1 3 d S ; A B C D . S A B C D + 1 3 d S ' ; A B C D . S A B C D
= 1 3 d S ; A B C D + d S ' ; A B C D . S A B C D = 1 3 S S ' . S A B C D = 2 S A B C D
Từ giả thiết suy ra ABCD là hình vuông, gọi a là cạnh hình vuông đó.
Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng r và ngoại tiếp hình vuông ABCD.
Suy ra 2 r = A C = a 2 ⇒ r = a 2 2 . Từ d I ; P 2 + r 2 = R 2 .
⇔ r = R 2 − d I ; P 2 = 3 2 − 8 3 2 = 17 3 = a 2 2 ⇔ a = 2 17 3 2
Vậy V H = 2 S A B C D = 2 a 2 = 2. 2 17 3 2 2 = 68 9 .