Con lắc thử đạn là một bao cát, khối lượng 19,9kg, treo vào một sợi dây có chiều dài là 2m. Khi bắn một đầu đạn khối lượng 100g theo phương nằm ngang, thì đầu đạn cắm vào bao cát và nâng bao cát lên cao theo một cung tròn là cho trọng tâm của bao cát sao cho dây treo bao cát hợp với phương thẳng đứng một góc
60
0
a. Xác định vận tốc v của viên đạn trước lúc va chạm vào...
Đọc tiếp
Con lắc thử đạn là một bao cát, khối lượng 19,9kg, treo vào một sợi dây có chiều dài là 2m. Khi bắn một đầu đạn khối lượng 100g theo phương nằm ngang, thì đầu đạn cắm vào bao cát và nâng bao cát lên cao theo một cung tròn là cho trọng tâm của bao cát sao cho dây treo bao cát hợp với phương thẳng đứng một góc 60 0
a. Xác định vận tốc v của viên đạn trước lúc va chạm vào bao cát.
b. Xác định năng lượng tỏa ra khi viên đạn găm vào bao cát
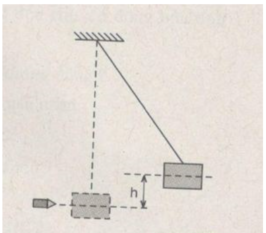
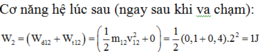
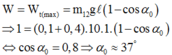
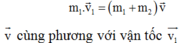
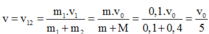
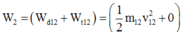
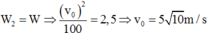
a. Chọn mốc thế năng là vị trí cân bằng của bao cát
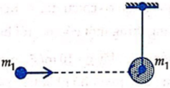
Vận tốc của bao cát và viên đạn ngay sau khi va chạm. Theo định luật bảo toàn cơ năng
W H = W A ⇒ 1 2 ( m + m 0 ) V H 2 = ( m + m 0 ) g z A M à z A = l − l cos 60 0 = l ( 1 − cos 60 0 ) ⇒ V H = 2 g l ( 1 − c o s 60 0 ) = 2.10.2 ( 1 − 1 2 ) = 2 5 ( m / s )
Theo định luật bảo toàn động lượng
m 0 v 0 = ( m + m 0 ) V H ⇒ v 0 = ( m + m 0 ) V H m 0 = ( 19 , 9 + 0 , 1 ) .2 5 0 , 1 = 400 5 ( m / s )
b. Độ biến thiên động năng
Δ W d = W d 2 − W d 1 = m + m 0 2 ( m 0 v 0 m + m 0 ) 2 − m 0 v 0 2 2 ⇒ Δ W d = ( m 0 m + m 0 − 1 ) m 0 v 0 2 2 = − m m + m 0 . m 0 . v 0 2 2
⇒ Δ W d = − 19 , 9 19 , 9 + 0 , 1 . 0 , 1. ( 400 5 ) 2 2 = − 39800 ( J )
Vậy năng lượng được chuyển hóa thành nhiệt năng là 39800 J