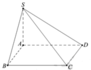
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và S A = a (tham khảo hình vẽ bên). Góc giữa hai mặt phẳng (SAB) và (SCD) bằng
A. 60 0
B. 45 0
C. 30 0
D. 90 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Phương pháp:
Xác định góc giữa hai mặt phẳng α , β :
- Tìm giao tuyến Δ của α , β .
- Xác định 1 mặt phẳng γ ⊥ Δ .
- Tìm các giao tuyến a = α ∩ γ , b = β ∩ γ
- Góc giữa hai mặt phẳng α , β : α ; β = a ; b .
Cách giải:
Ta có: S C D ∩ A B C D = C D
Mà C D ⊥ A D (ABCD là hình vuông), C D ⊥ S A (vì S A ⊥ A B C D ) ⇒ C D ⊥ S A D
S C D ∩ S A D = S D ,
A B C D ∩ S A D = A D ⇒ S C D , A B C D = S D ; A D = S D A

Đáp án A
Do AB // CD => giao tuyến của mặt phẳng (SAB) và (SCD) là đường thẳng qua S và song song với AB.
Dễ thấy Sx ⊥ (DSA) => Góc tạo bởi mặt phẳng (SAB) và (SCD) bằng góc D S A ^ = a r c tan 1 3 = 30 0

Đáp án B
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .
Đáp án B