Trong mặt phẳng tọa độ , cho tam giác MNP có M(1;-1) : N(5; -3) và P thuộc trục Oy, trọng tâm G của tam giác nằm trên trục Ox.Toạ độ của điểm P là
A.(0;4)
B.(4;0)
C.(2;4)
D.(2;0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\overrightarrow {OM} = \left( {2;1} \right),\overrightarrow {MN} = \left( { - 3;2} \right),\overrightarrow {MP} = \left( {2;1} \right)\)
b) Ta có: \(\overrightarrow {MN} .\overrightarrow {MP} = - 3.2 + 2.1 = - 4\)
c) Ta có: \(MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( { - 3} \right)}^2} + {2^2}} = \sqrt {13} ,MP = \left| {\overrightarrow {MP} } \right| = \sqrt {{2^2} + {1^2}} = \sqrt 5 \)
d) Ta có: \(\cos \widehat {MNP} = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{\left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {MP} } \right|}} = \frac{- 4}{{\sqrt {13} .\sqrt 5 }} = \frac{- 4}{{\sqrt {65} }}\)
e) Tọa độ trung điểm I của đoạn NP là: \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_N} + {x_P}}}{2} = \frac{3}{2}\\{y_I} = \frac{{{y_N} + {y_P}}}{2} = \frac{5}{2}\end{array} \right. \Leftrightarrow I\left( {\frac{3}{2};\frac{5}{2}} \right)\)
Tọa độ trọng tâm G của tam giác MNP là: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_M} + {x_N} + {x_P}}}{3}\\{y_G} = \frac{{{y_M} + {y_N} + {y_P}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_G} = \frac{5}{3}\\{y_C} = 2\end{array} \right. \Leftrightarrow G\left( {\frac{5}{3};2} \right)\)

Chọn D.
M(-5;6), N(-4;-1), P(4;3)
Gọi H(x;y) là trực tâm ∆ MNP, ta có:
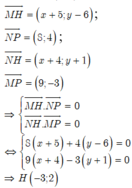

Ta có 3 điểm M ( 8;3 ), N ( 1;4 ), P ( 5;x ) ⇒ M P → - 3 ; x ; - 3 , N P → 4 ; x ; - 4
∆ M N P vuông tại P ⇔ M P → . N P → = 0 ⇔ - 12 + x - 3 x - 4 = 0 ⇔ x = 0 ; x = 7 .
Đáp án B

Chọn B.
Ta có 3 điểm M(8;3), N(1;4), P(5;x)
![]()
Để ∆ MNP vuông tại P
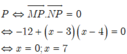
Đáp án A