x 2 + x y x 3 + x 2 y + x y 2 + y 3 + y x 2 + y 2 : 1 x - y - 2 x y x 3 - x 2 y + x y 2 - y 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
T
19 tháng 9 2023
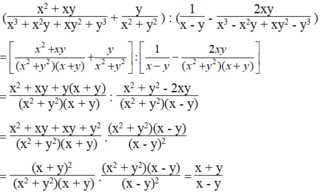
\(B=\left(x+y\right)^3+3\left(x-y\right)\left(x+y\right)^2+3\left(x-y\right)^2\left(x+y\right)+\left(x-y\right)^3\)
\(=\left(x+y\right)^3+3\cdot\left(x+y\right)^2\cdot\left(x-y\right)+3\cdot\left(x+y\right)\cdot\left(x-y\right)^2+\left(x-y\right)^3\)
\(=\left[\left(x+y\right)+\left(x-y\right)\right]^3\)
\(=\left(x+y+x-y\right)^3\)
\(=\left(2x\right)^3\)
\(=8x^3\)
\(---\)
\(C=8\left(x+2y\right)^3-6\left(x+2y\right)^2x+12\left(x+2y\right)x^2-8x^3\) (sửa đề)
\(=\left[2\left(x+2y\right)\right]^3-3\cdot\left(x+2y\right)^2\cdot2x+3\cdot\left(x+2y\right)\cdot\left(2x\right)^2-\left(2x\right)^3\)
\(=\left[2\left(x+2y\right)-2x\right]^3\)
\(=\left(2x+4y-2x\right)^3\)
\(=\left(4y\right)^3\)
\(=64y^3\)
\(---\)
\(D=\left(x-y\right)^3-3\cdot\dfrac{\left(x-y\right)^2}{2}\cdot y+3\cdot\dfrac{\left(x-y\right)}{4}\cdot y^2-\dfrac{y^3}{8}\)
\(=\left(x-y\right)^3-3\cdot\left(x-y\right)^2\cdot\dfrac{y}{2}+3\cdot\left(x-y\right)\cdot\left(\dfrac{y}{2}\right)^2-\left(\dfrac{y}{2}\right)^3\)
\(=\left[\left(x-y\right)-\dfrac{y}{2}\right]^3\)
\(=\left(x-y-\dfrac{y}{2}\right)^3\)
\(=\left(x-\dfrac{3}{2}y\right)^3\)
#\(Toru\)
E
22 tháng 9 2019
thực hiện nhân đa thức với đa thức ở vế trái xog rút gọn là nó = vế pải
TL
24 tháng 9 2019
1/ Biến đổi vế trái , ta có :
(x-y)(x+y)= x2+xy - xy-y2= x2-y2
=> (x-y) (x+y) =x2-y2
2/ Biến đổi vế trái , ta có :
(x-y) (x2+xy+y2)= x3+x2y+xy2-x2y-xy2-y3
= (x2y-x2y)+(xy2-xy2)+x3-y3=x3-y3
=> (x-y) (x2+xy+y2) =x3-y3
3/ / Biến đổi vế trái , ta có :
(x+y) (x2-xy+y2) =x3-x2y+xy2+x2y-xy2+y3
(-x2y+x2y) + ( xy2-xy2) + x3+y3= x3+y3
NT
2
21 tháng 6 2023
a: =2(x-y)^3/(x-y)-7(x-y)^2/(x-y)+(x-y)/(x-y)
=2(x-y)^2-7(x-y)+1
b: =3(x-y)^5/5(x-y)^2-2(x-y)^4/5(x-y)^2+3(x-y)^2/5(x-y)^2
=3/5(x-y)^3-2/5(x-y)^2+3/5
21 tháng 6 2023
\(a,\)
\(\left[2\left(x-y\right)^3-7\left(y-x\right)^2-\left(y-x\right)\right]:\left(x-y\right)\)
\(=\left[2\left(x-y\right)^3-7\left(x-y\right)^2+\left(x-y\right)\right]:\left(x-y\right)\)
\(=\left\{\left(x-y\right)\left[2\left(x-y\right)^2-7\left(x-y\right)+1\right]\right\}:\left(x-y\right)\)
\(=2\left(x-y\right)^2-7\left(x-y\right)+1\)
\(b,\)
\(\left[3\left(x-y\right)^5-2\left(x-y\right)^4+3\left(x-y\right)^2\right]:\left[5\left(x-y\right)^2\right]\)
\(=\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\)
TT
20 tháng 10 2020
\(A=\left(x+y\right)^2+\left(x-y\right)^2+2\left(x+y\right)\left(x-y\right)\)
\(=x^2+2xy+y^2+x^2-2xy+y^2+2\left(x^2-y^2\right)\)
\(=2x^2+2x^2=4x^2\)
Vs x = 1/2 ; y = 3 ⇒ \(A=\frac{1}{4}.4=1\)
\(B=3x^2-6xy+y^2-2x^2-4xy-2y^2-x^2+y^2=-10xy=\frac{1}{2}.3.10=15\)
\(C=x^3+3x^2y+3xy^2+y^2-x^3+3x^2y-3xy^2+y^3-6x^2y-1=2y^2-1=18-1=17\)\(D=x^3+y^3-x^3-3x^2y-3xy^2-y^3=-3x^2y-3xy^2=\frac{1}{4}.9+\frac{1}{2}.27=\frac{9}{4}+\frac{108}{4}=\frac{117}{4}\)Check lại nhé <33 sợ sai lém
25 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`1,`
\((y-5)(y+8)-(y+4)(y-1)\)
`= y(y+8) - 5(y+8) - [y(y-1) + 4(y-1)]`
`= y^2+8y - 5y - 40 - (y^2-y + 4y - 4)`
`= y^2+8y-5y-40 - y^2+y-4y+4`
`= (y^2-y^2)+(8y-5y+y-4y) +(-40+4)`
`= -36`
Vậy, bt trên không phụ thuộc vào gtr của biến.
`2,`
\(y^4-(y^2+1)(y^2-1)\)
`= y^4 - [y^2(y^2-1)+y^2-1]`
`= y^4- (y^4-y^2 + y^2-1)`
`= y^4-(y^4-1)`
`= y^4-y^4+1`
`= 1`
Vậy, bt trên không phụ thuộc vào gtr của biến.
`3,`
\(x(y-z) + y(z-x) +z(x-y)\)
`= xy-xz + yz - yx + zx-zy`
`= (xy-yx) + (-xz+zx) + (yz-zy)`
`= 0`
Vậy, bt trên không phụ thuộc vào gtr của biến.
`4,`
\(x(y+z-yz) -y(z+x-xz)+z(y-x)\)
`= xy+xz-xyz - yz - yx + yxz + zy - zx`
`= (xy-yx)+(xz-zx)+(-xyz+yxz)+(-yz+zy)`
`= 0`
Vậy, bt trên không phụ thuộc vào gtr của biến.
`5,`
\(x(2x+1)-x^2(x+2)+x^3-x+3\)
`= 2x^2+x - x^3 - 2x^2 + x^3 - x + 3`
`= (2x^2-2x^2)+(-x^3+x^3)+(x-x)+3`
`= 3`
Vậy, bt trên không phụ thuộc vào gtr của biến.
`6,`
\(x(3x-x+5)-(2x^3+3x-16)-x(x^2-x+2)\)
`= 3x^2 - x^2 + 5x - 2x^3 - 3x + 16 - x^3 + x^2 - 2x`
`= -3x^3 + 3x^2 + 16`
Bạn xem lại đề bài.
`\text {#KaizuulvG}`
T
24 tháng 8 2023
Sửa đề: Các dấu bằng ở yêu cầu là dấu cộng.
1. Có: \(x+y=3\)
\(\Leftrightarrow\left(x+y\right)^2=3^2\)
\(\Leftrightarrow x^2+2xy+y^2=9\)
\(\Leftrightarrow x^2+y^2=9-2\cdot1=7\) (do \(xy=1\))
\(------\)
Lại có: \(x+y=3\)
\(\Leftrightarrow\left(x+y\right)^3=3^3\)
\(\Leftrightarrow x^3+y^3+3xy\left(x+y\right)=27\)
\(\Leftrightarrow x^3+y^3+3\cdot1\cdot3=27\) (do x + y = 3; xy = 1)
\(\Leftrightarrow x^3+y^3=18\)
Ta có: \(x^2+y^2=7\)
\(\Leftrightarrow\left(x^2+y^2\right)^2=7^2\)
\(\Leftrightarrow x^4+y^4+2\cdot\left(xy\right)^2=49\)
\(\Leftrightarrow x^4+y^4=49-2\cdot1=47\) (do xy = 1)
24 tháng 3 2020
a) Ta có: \(\frac{\left[2\left(y-x\right)^3-2\left(y-x\right)^2+\left(x-y\right)\right]}{y-x}\)
\(=\frac{2\left(y-x\right)^3}{y-x}-\frac{2\left(y-x\right)^2}{y-x}+\frac{x-y}{y-x}\)
\(=2\left(y-x\right)^2-2\left(y-x\right)-1\)
\(=2y^2-4yx+2x^2-2y+2x-1\)
