Viết phương trình mặt phẳng ( α ) trong các trường hợp sau: ( α ) đi qua ba điểm M(1; 1; 1), N(4; 3; 2), P(5; 2; 1).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình ( α ) có dạng: (x – 2) + (y) + (z – 1) = 0 hay x + y + z – 3 = 0

Hai vecto có giá song song với mặt phẳng ( α ) là: u → = (0; 1; 1) và v → = (−1; 0; 2).
Suy ra ( α ) có vecto pháp tuyến là n → = u → ∧ v → = (2; −1; 1)
Mặt phẳng ( α ) đi qua điểm A(1; 0; 0) và nhận n → = (2; −1; 1) là vecto pháp tuyến. Vậy phương trình của (α) là: 2(x – 1) – y + z = 0 hay 2x – y + z – 2 = 0

∆ ⊥ ( α ) ⇒ a ∆ → = a α → = (2; −1; 1)
Phương trình tham số của ∆ là
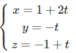
Phương trình chính tắc của ∆ là:
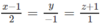

Đường thẳng d vuông góc với mp α x+y-z+5=0 nên đường thẳng d có vecto chỉ phương n → = 1 ; 1 ; - 1
Vậy pt tham số của đường thẳng d là: x = 2 + t y = - 1 + t z = 3 - t

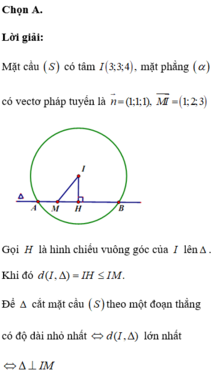




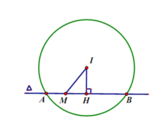

Hai vecto có giá song song hoặc nằm trên ( α ) là: MN → = (3; 2; 1) và MP → = (4; 1; 0).
Suy ra ( α ) có vecto pháp tuyến là n → = MN → ∧ MP → = (−1; 4; −5)
Vậy phương trình của ( α ) là: -1(x – 1) + 4(y – 1) – 5(z – 1) = 0 hay x – 4y + 5z – 2 = 0