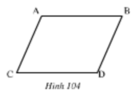
Trên hình 104 ta có AB // CD, AC // BD. Hãy chứng minh rằng AB = CD, AC = BD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
3
QD
20 tháng 4 2017
Vẽ đoạn thẳng AD.
∆ADB và ∆DAC có:
ˆA1A1^= ˆD1D1^(so le trong AB//CD)
AD là cạnh chung.
A2^=D2^(So le trong, AC//BD)
Do đó ∆ADB=∆DAC(g.c .g)
Suy ra: AB=CD, BD=AC
Xem thêm tại: http://loigiaihay.com/bai-38-trang-124-sach-giao-khoa-toan-7-tap-1-c42a5073.html#ixzz4elm8F0eT
6 tháng 8 2017
Vẽ đoạn thẳng AD.
∆ADB và ∆DAC có:
\(\widehat{A^1}\)= \(\widehat{D^1}\)(so le trong AB//CD)
AD là cạnh chung.
\(\widehat{A^2}\)=\(\widehat{D^2}\)(So le trong, AC//BD)
Do đó ∆ADB=∆DAC(g.c .g)
Suy ra: AB=CD, BD=AC
LV
30 tháng 4 2020
Lấy M là trung điểm của CD
AC2−AD2=BC2−BD2
<=> (AC−→−−AD−→−)(AC−→−+AD−→−)=(BC−→−−BD−→−)(BC−→−+BD−→−)
<=> 2.DC−→−.AM−→−=2.DC−→−.BM−→−
<=> 2.DC−→−.(AM−→−−BM−→−)=0
<=> 2.DC−→−.AB−→−=0
<=> DC vuông góc với AB
CM
30 tháng 7 2017
a) Ta có:
AB = AD (gt) ⇒ A thuộc đường trung trực của BD
CB = CD (gt) ⇒ C thuộc đường trung trực của BD
Vậy AC là đường trung trực của BD
b) Xét ΔABC và ΔADC có:
AB = AD (gt)
BC = DC (gt)
AC cạnh chung
⇒ ΔABC = ΔADC (c.c.c)
CM
18 tháng 3 2018
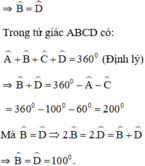
Vì PM là đường trung bình của tam giác DAB nên:
PM = AB/2 (tính chất đường trung bình tam giác)
Vì PN là đường trung bình của tam giác ΔACD nên:
PN = CD/2 (tính chất đường trung hình tam giác)
Mà PN = PM + MN
Suy ra: MN = PN – PM = CD/2 - AB/2 = (CD-AB)/2
CM
26 tháng 3 2019
Gọi P là trung điểm của AD, nối PM
Trong ΔDAB ta có: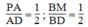 
Suy ra: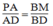 
Suy ra: PM // AB (Định lí đảo của định lí Ta-lét) (1)
Trong
△
ACD, ta có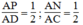 
Suy ra: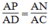 
Suy ra: PN // CD (định lí đảo định lí Ta-lét) (2)
Từ (1) và (2) và theo tiên đề Ơ-clít suy ra P, M, N thẳng hàng.
Vậy MN // CD hay MN // AB.
Kí hiệu góc như hình dưới:
Vẽ đoạn thẳng AD
Xét ΔABD và ΔDCA có:
⇒ ΔADB = ΔDAC ( g.c.g)
⇒ AB = CD ; BD = AC (hai cạnh tương ứng).