Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy M là trung điểm của CD
AC2−AD2=BC2−BD2
<=> (AC−→−−AD−→−)(AC−→−+AD−→−)=(BC−→−−BD−→−)(BC−→−+BD−→−)
<=> 2.DC−→−.AM−→−=2.DC−→−.BM−→−
<=> 2.DC−→−.(AM−→−−BM−→−)=0
<=> 2.DC−→−.AB−→−=0
<=> DC vuông góc với AB

Kí hiệu góc như hình dưới:
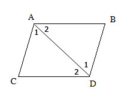

Vẽ đoạn thẳng AD
Xét ΔABD và ΔDCA có:

⇒ ΔADB = ΔDAC ( g.c.g)
⇒ AB = CD ; BD = AC (hai cạnh tương ứng).

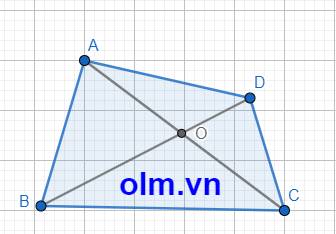
Xét \(\Delta\)AOD ta có: AO + OD > AD (trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét \(\Delta\) OCD ta có: BO + OC > BC ( trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AO + OD + BO + OC > AD + BC
(AO + OC) + ( OD + OB > AD + BC
AC+ BD > AD + BC
Chứng Minh tương tự ta có: AC + BD > AB + CD