Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Chứng minh MB\(\perp\)MC
Xét ΔABM vuông tại A và ΔDMC vuông tại D có
AB=DM
AM=DC
Do đó: ΔABM=ΔDMC
=>\(\widehat{AMB}=\widehat{DCM}\)
mà \(\widehat{DCM}+\widehat{DMC}=90^0\)
nên \(\widehat{AMB}+\widehat{DMC}=90^0\)
\(\widehat{AMB}+\widehat{BMC}+\widehat{DMC}=180^0\)
=>\(\widehat{BMC}+90^0=180^0\)
=>\(\widehat{BMC}=90^0\)
=>MB\(\perp\)MC

TAm giác AOB cuông tại O , theo py ta go
=> AB^2 = OA^2 + OB^2
Tương tự CD^2 = OC^2 + OD^2
BC^2 = OB^2 + OC^2
AD^2 = OA^2 + OD^2
AB^2 + CD^2 = OA^2 + OB^2 + OC^2 + CD^2 = BC^2 + AD^2 ( ĐPCM)

Trước hết, hình thang cân ABCD có 2 đường chéo vuông góc với nhau nên nó là hình vuông.
Do đó H trùng với D ( cùng là đường cao hình thang )
Do đó AH=AD
Mà AB+CD=AD+AD
⇒2AH=AB+CD
⇒\(AH=\frac{AB+CD}{2}\)
Vậy \(AH=\frac{AB+CD}{2}\)

GT : ABCD là hình thang ( AB< CD)
MA = MD
MN//AB//DC
KL: CM: N,E,F lần lượt là trung điểm của BC, BD,AC
Giải:
Xét hình thang ABCD có :
MA=MD ( gt)
MN//AB//DC ( gt)
=> MN là đường trung bình của hình thang ABCD
=> NB=NC
=> N là trung điểm của BC
Xét tam giác ABD có :
MA=MD ( gt)
MN//AB (gt) hay ME//AB(vì ME thuộc MN)
=> ME là đường trung bình của tam giác ABD
=> EB=ED
=> E là trung điểm của BD
Xét tam giác ABC có:
NB= NC ( cmt)
MN//AB ( gt ) hay FN//AB ( vì FN thuộc MN )
=> NF là đường trung bình của tam giác ABC
=> NB=NC
=> N là trung điểm của BC

Kí hiệu góc như hình dưới:
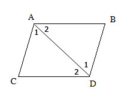

Vẽ đoạn thẳng AD
Xét ΔABD và ΔDCA có:

⇒ ΔADB = ΔDAC ( g.c.g)
⇒ AB = CD ; BD = AC (hai cạnh tương ứng).
Lấy M là trung điểm của CD
AC2−AD2=BC2−BD2AC2−AD2=BC2−BD2
<=> (AC−→−−AD−→−)(AC−→−+AD−→−)=(BC−→−−BD−→−)(BC−→−+BD−→−)(AC→−AD→)(AC→+AD→)=(BC→−BD→)(BC→+BD→)
<=> 2.DC−→−.AM−→−=2.DC−→−.BM−→−2.DC→.AM→=2.DC→.BM→
<=> 2.DC−→−.(AM−→−−BM−→−)=02.DC→.(AM→−BM→)=0
<=> 2.DC−→−.AB−→−=02.DC→.AB→=0
<=> DC vuông góc với AB