Cho tam giác ABC vuông tại A có AB : AC = 4 : 5 và đường cao AH bằng 12cm. Khi đó độ dài đoạn thẳng HB bằng
A. 6cm; B. 9,6cm; C. 12cm; D. 15cm.
Hãy chọn phương án đúng.
*Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác ABC vuông tại A có đường cao AH:
AB = c, AC = b, BC = a, AH = h, BH = c’, CH = b’.

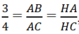
Hướng dẫn:
∆ ABC ∼ ∆ HBA nên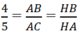
Suy ra HB = 4/5HA = 48/5 = 9,6. Chọn B.