Chứng minh các đẳng thức sau: 5 x - 5 x 2 - 1 = 5 x + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

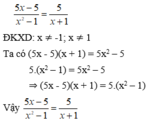

x^5- 1/ x-1= x^4+ x^3+ x^2+ x+ 1
<=> x^5 - 1 = (x - 1)(x^4 + x^3 + x^2 + x + 1)
<=> x^5 - 1 = x^5 + x^4 + x^3 + x^2 + x - x^4 - x^3 - x^2 - x - 1
<=> x^5 - 1 = x^5 - 1 (đúng)
=> đpcm
Viết lại cho vui ạ:))
\(\dfrac{x^5-1}{x-1}=x^4+x^3++x^2+x+1\\ \Leftrightarrow x^5-1=\left(x-1\right)\left(x^4+x^3+x+1\right)\\ \Leftrightarrow x^5-1=x^5+x^4+x^3+x^2+x-x^4-x^3-x^2-x-1\\ \Leftrightarrow x^5-1=x^5-1\left(đpcm\right)\)


a/ ĐK: $x\ne -5$
$\dfrac{6x^2+30x}{4}=\dfrac{6x(x+5)}{4}=\dfrac{3x(x+5)}{2}$
Đề này sai
b/ ĐK: $x\ne \pm 1$
$\dfrac{(x+2)(x+1)}{x^2-1}\\=\dfrac{(x+2)(x+1)}{(x-1)(x+1)}\\=\dfrac{x+2}{x-1}$
$\to$ ĐPCM

a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(=x^2+2x-5x-10+3x^2-12-3x+\dfrac{1}{2}x^2+5x^2\)
\(=\dfrac{19}{2}x^2-6x-22\)
Vậy biểu thức trên phụ thuộc vào biến x.
b) \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\)
Giải:
VT = \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3+y^2+y-y^2-y-1\)
\(=y^3-1\)
Vậy \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\).
Giải:
a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3\left(x^2-4\right)-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3x^2-12x-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=-10-18x+\dfrac{19}{2}x^2\)
Vậy biểu thức trên phụ thuộc vào biễn x
b) \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3-y^2+y^2-y+y-1\)
\(=y^3-\left(y^2-y^2\right)-\left(y-y\right)-1\)
\(=y^3-1\)
Vậy ...

\(\sqrt{x-2\sqrt{x-1}}+\sqrt{x+2\sqrt{x-1}}\)
\(=\sqrt{x-1-2\sqrt{x-1+1}}+\sqrt{x-1+2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}-1\right)^2}+\sqrt{\left(\sqrt{x-1}+1\right)^2}\)
\(=\left|\sqrt{x-1}-1\right|+\left|\sqrt{x-1}+1\right|\)
\(=\sqrt{x-1}-1+\sqrt{x-1}+1\left(x\ge2\right)=2\sqrt{x-1}\)
a) \(\dfrac{1}{\sqrt{5}+\sqrt{7}}=\dfrac{\sqrt{7}-\sqrt{5}}{\left(\sqrt{5}+\sqrt{7}\right)\left(\sqrt{7}-\sqrt{5}\right)}=\dfrac{\sqrt{7}-\sqrt{5}}{2}\)
c) \(\dfrac{7}{\sqrt{5}-\sqrt{3}+\sqrt{5}}=\dfrac{7}{2\sqrt{5}-\sqrt{3}}=\dfrac{7\left(2\sqrt{5}+\sqrt{3}\right)}{\left(2\sqrt{5}+\sqrt{3}\right)\left(2\sqrt{5}-\sqrt{3}\right)}\)
\(=\dfrac{14\sqrt{5}+7\sqrt{3}}{17}\)


a: \(\dfrac{x^2-3x+2}{x^2-1}=\dfrac{\left(x-2\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-2}{x+1}\)
\(a,VP=\dfrac{\left(x-1\right)\left(x-2\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-2}{x+1}=VP\\ b,VT=\dfrac{u\left(4u^2-1\right)}{5\left(1-2u\right)}=\dfrac{-u\left(1-2u\right)\left(1+2u\right)}{5\left(1-2u\right)}=\dfrac{-u\left(1+2u\right)}{5}=-\dfrac{2u^2+u}{5}=VP\)