Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
[Phương pháp tự luận]
Ta có y ' = 6 x 2 - 18 x + 12
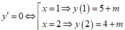
A ( 1 ; 5 + m ) v à B ( 2 ; 4 + m ) là hai điểm cực trị của đồ thị hàm số
Chu vi của ∆ O A B là
Sử dụng tính chất u + v ≥ u + v
Từ đó ta có :
Dấu bằng xảy ra khi và chỉ khi u , v cùng hướng
Vậy chu vi ∆ O A B nhỏ nhất bằng ( 10 + 2 ) khi m = - 14 3
`y'=3x^2+4mx=0<=>[(x=0),(x=-4/3m):}` `(m ne 0)`
`=>[(y=-m),(y=32/27 m^3-m):}`
`=>A(0;-m),B(-4/3m;32/27 m^3-m)`
Để `\triangle OAB` vuong tại `O`
`=>\vec{OA}.\vec{OB}=0`
`<=>(0;-m).(-4/3m;32/27 m^3 -m)=0`
`<=>0.(-4/3m)-m(32/27 m^3-m)=0`
`<=>m^2(32/27m^2 -1)=0`
`<=>[(m=0(L)),(m=+-[3\sqrt{6}]/8 (t//m)):}`
Vậy `m=+-[3\sqrt{6}]/8`.
Ta có \(y'=6x^2-18x+12;y'=0\Leftrightarrow x^2-3x+2=0\Leftrightarrow x=1\) hoặc \(x=2\)
\(\Rightarrow y=5+m\) hoặc \(y=4+m\)
Gọi \(A\left(1;5+m\right);B\left(2;4+m\right)\) là 2 điểm cực trị của đồ thị hàm số
Ta có : \(\overrightarrow{AB}=\left(1;-1\right);\overrightarrow{OA}=\left(1;5+m\right)\). A, B, O không thẳng hàng khi và chỉ khi vectơ \(\overrightarrow{AB};\overrightarrow{OA}\) không cùng phương khi và chỉ khi \(5+m\ne-1\Leftrightarrow m\ne-6\)(*)
Ta có : \(OA=\sqrt{1+\left(5+m\right)^2};OB=\sqrt{4+\left(4+m\right)^2};AB=\sqrt{2}\)
Chu vi tam giác OAB :
\(P_{OAB}=OA+OB+AB=\sqrt{1+\left(5+m\right)^2}+\sqrt{4+\left(4+m\right)^2}+\sqrt{2}\)
\(P_{OAB}\) đạt giá trị nhỏ nhất khi và chỉ khi \(\sqrt{1+\left(5+m\right)^2}+\sqrt{4+\left(4+m\right)^2}\) đạt giá trị nhỏ nhất
Đặt \(u'\left(1;5-m\right);v'\left(2;4+m\right)\) ta có :
\(\left|\overrightarrow{u'}\right|+\left|\overrightarrow{v'}\right|=\sqrt{1+\left(-5+m\right)^2}+\sqrt{4+\left(4+m\right)^2}=\sqrt{1+\left(5+m\right)^2}+\sqrt{4+\left(4+m\right)^2}\)
Mặt khác \(\left|\overrightarrow{u'}\right|+\left|\overrightarrow{v'}\right|\ge\left|\overrightarrow{u'}+\overrightarrow{v'}\right|\Rightarrow\sqrt{1+\left(-5+m\right)^2}+\sqrt{4+\left(4+m\right)^2}\ge\sqrt{3^2+\left(-1\right)^2}=\sqrt{10}\)
Dấu "=" xảy ra khi và chỉ khi \(\left|\overrightarrow{u'}\right|;\left|\overrightarrow{v'}\right|\) cùng hướng
\(\Leftrightarrow0< \frac{1}{2}=\frac{-5-m}{4+m}\Leftrightarrow m=-\frac{14}{3}\) (thỏa mãn (*))
Vậy với \(m=-\frac{14}{3}\) thì đồ thị hàm số (1) có các điểm cực đại, cực tiểu cùng gốc tọa độ O tạo thành một tam giác có chu vi nhỏ nhất.
Chọn D.
Phương pháp:
Giải phương trình hoành độ giao điểm, tìm giao điểm của hai đồ thị.
Dựa vào công thức trọng tâm, xác định m.
Cách giải:
Phương trình hoành độ giao điểm của d và (C) là
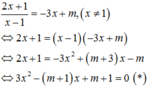
Để d cắt (C) tại hai điểm phân biệt A, B thì (*) có 2 nghiệm phân biệt khác 1
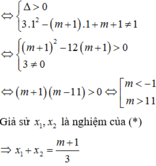
+ Đạo hàm y’ = 6x2 – 18x+ 12
+ Tọa độ hai điểm cực trị của đồ thị hàm số là A( 1; 5+m) và B( 2; 4+ m)
O ; A và B không thẳng hàng nên – 4-m≠ 2 hay m≠ - 6
Chu vi của tam giác OAB là:
Dấu bằng xảy ra khi và chỉ khi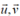
cùng hướng 
.
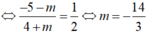Vậy chu vi tam giác OAB nhỏ nhất bằng (√10 + √2) khi m= -14/ 3.
Chọn C.