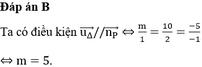Tìm giá trị của x để 22 x ¯ ⋮ 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

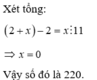

a) Rút gọn thu được B = 4 x ( 2 + x ) ( 2 − x ) ( 2 + x ) : x − 3 x ( 2 − x ) = 4 x 2 x − 3 với x ≠ ± 2 ; x ≠ 0 ; x ≠ 3
b) 4 x 2 x − 3 < 0 ⇔ x − 3 < 0 ⇔ x < 3 ;
Kết hợp điều kiện được 0 < x < 3; x ≠ ± 2.

Tìm được A = 24 5 và B = - 6 x - 4 với x > 0 và x ≠ 4 ta tìm được 0 < x < 1
Ta có M = - 1 + 2 x ∈ Z => x ∈ Ư(2) từ đó tìm được x=1

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn. Viết như thế này khó quan sát quá.

Đáp án D.
Phương trình tương đương với

Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t ( x ) luôn đồng biến trên 0 ; 1 . Suy ra min x ∈ 0 ; 1 t ( x ) = t ( 0 ) = 0 và max x ∈ 0 ; 1 t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng:
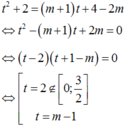
Phương trình (1) có nghiệm t ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.

Ta có
\(C=\frac{12-3x}{4-x}+\frac{10}{4-x}=3+\frac{10}{4-x}\)
C lớn nhất <=> \(\frac{10}{4-x}\) lớn nhất <=> 4 - x bé nhất >0
Mà x nguyên
=>x=1
Thay vào ta có \(C=\frac{22-3.1}{4-1}=\frac{19}{4}\)
Vậy MAX(C)=19/4 khi x=1
C=\(\frac{22-3x}{4-x}=3+\frac{10}{4-x}\)để C lớn nhất thì \(\frac{10}{4-x}\) lớn nhất
mà x nguyên=> 4-x=1=> x=3
vậy GTLN của C=13 khi x=1

Điều kiện : \(x\ne4\)
Biểu diễn : \(C=\frac{22-3x}{4-x}=\frac{3\left(4-x\right)+10}{4-x}=\frac{10}{4-x}+3\)
Ta có C đạt giá trị lớn nhất \(\Leftrightarrow\frac{10}{4-x}\)đạt giá trị lớn nhất \(\Leftrightarrow4-x\)đạt giá trị nhỏ nhất
Đến đây ta xét các trường hợp :
1. Với \(x>4\Rightarrow4-x< 0\Rightarrow\frac{10}{4-x}< 0\)
2. Với \(0\le x\le3\) \(\Rightarrow\frac{5}{2}\le\frac{10}{4-x}\le10\)
3. Với \(x< 0\), xét \(f\left(x\right)=4-x\) có giá trị càng tăng khi x càng giảm (x < 0) , do đó f(x) nhỏ nhất tại x = -1
\(\Rightarrow\frac{10}{4-x}=2\)
So sánh các trường hợp , được \(MaxC=13\Leftrightarrow x=3\)

Ta có: 4 - x \(\ne\)0 \(\Leftrightarrow\) x \(\ne\)4
C = \(\frac{12-3x+10}{4-x}\)=\(\frac{3\left(4-x\right)}{4-x}+\frac{10}{4-x}\)= \(3+\frac{10}{4-x}\)
Để C đạt GTLN thì \(\frac{10}{4-x}\)phải là GTLN, mà 10 là số nguyên dương nên 4 - x phải nguyên dương nhỏ nhất.
\(\Rightarrow\)4 - x = 1
\(\Leftrightarrow\)x = 3
Khi do: C = 13
Vậy GTLN của C =13 khi x = 3

A = \(\dfrac{22-3x}{4-x}\)
A = \(\dfrac{3.\left(4-x\right)+10}{4-x}\)
A = 3 + \(\dfrac{10}{4-x}\)
A lớn nhất khi \(\dfrac{10}{4-x}\) lớn nhất. Vì 10 > 0; \(x\) \(\in\) Z nên \(\dfrac{10}{4-x}\) lớn nhất khi
4 - \(x\) = 1 ⇒ \(x\) = 4 - 1 ⇒ \(x\) = 3
Vậy Amin = 3 + \(\dfrac{10}{1}\) = 13 khi \(x\) =3
Kết luận giái trị lớn nhất của biểu thức là 13 xảy ra khi \(x\) = 3