Cho biểu thức:
A = a 2 - 1 2 a 2 a - 1 a + 1 - a + 1 a - 1
b) Tìm a để A < 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

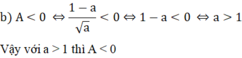

a,ĐK : \(a\ne\pm1\)
\(K=\left(\frac{a}{a-1}-\frac{1}{a^2-a}\right):\left(\frac{1}{a+1}+\frac{2}{a^2-1}\right)\)
\(=\left(\frac{a}{a-1}-\frac{1}{a\left(a-1\right)}\right):\left(\frac{1}{a+1}+\frac{2}{\left(a-1\right)\left(a+1\right)}\right)\)
\(=\left(\frac{a^2}{a\left(a-1\right)}-\frac{1}{a\left(a-1\right)}\right):\left(\frac{a-1}{\left(a+1\right)\left(a-1\right)}+\frac{2}{\left(a+1\right)\left(a-1\right)}\right)\)
\(=\left(\frac{\left(a-1\right)\left(a+1\right)}{a\left(a-1\right)}\right):\left(\frac{a+1}{\left(a+1\right)\left(a-1\right)}\right)\)
\(=\frac{a+1}{a}.\frac{a-1}{1}=\frac{a^2-1}{a}\)
b, Thay a = 1/2 ta được :
\(K=\frac{\left(\frac{1}{2}\right)^2-1}{\frac{1}{2}}=\frac{\frac{1}{4}-1}{\frac{1}{2}}=\frac{-\frac{3}{4}}{\frac{1}{2}}=-\frac{3}{8}\)

\(a.a\ne\pm1\)
\(b.K=\dfrac{1}{a+1}+\dfrac{2}{a^2-1}=\dfrac{a-1}{\left(a-1\right)\left(a+1\right)}+\dfrac{2}{\left(a-1\right)\left(a+1\right)}=\dfrac{a+1}{\left(a-1\right)\left(a+1\right)}=\dfrac{1}{a-1}\)
\(c.K=\dfrac{1}{1-\dfrac{1}{2}}=\dfrac{1}{\dfrac{1}{2}}=2\)

Bài 1:
a: \(A=\dfrac{x^2-3+x+3}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x}=\dfrac{x\left(x+1\right)}{x\left(x-3\right)}=\dfrac{x+1}{x-3}\)
b: Để A=3 thì 3x-9=x+1
=>2x=10
hay x=5
Bài 2:
a: \(A=\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x+2-x}{x+2}\)
\(=\dfrac{-6}{x-2}\cdot\dfrac{1}{2}=\dfrac{-3}{x-2}\)
b: Để A nguyên thì \(x-2\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{3;1;5;-1\right\}\)

a) \(A=\dfrac{3\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}-\dfrac{\sqrt{a}+1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}-\dfrac{\sqrt{a}-3}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{3\sqrt{a}-3-\sqrt{a}-1-\sqrt{a}+3}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{\sqrt{a}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{1}{\sqrt{a}+1}\)
b) Với \(a=3-2\sqrt{2}\)(tmđk)
\(A=\dfrac{1}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{\sqrt{a}-1}{a-1}\)
\(=\dfrac{\sqrt{3-2\sqrt{2}}-1}{3-2\sqrt{2}-1}=\dfrac{\sqrt{\left(\sqrt{2}-1\right)^2}-1}{2-2\sqrt{2}}=\dfrac{\left|\sqrt{2}-1\right|-1}{2-2\sqrt{2}}=\dfrac{\sqrt{2}-1-1}{2-2\sqrt{2}}=\dfrac{\sqrt{2}-2}{2-2\sqrt{2}}=\dfrac{\sqrt{2}\left(1-\sqrt{2}\right)}{2\left(1-\sqrt{2}\right)}=\dfrac{\sqrt{2}}{2}\)

a) ĐKXĐ: a2-1 ≠0 ⇔ (a-1)(a+1)≠0 ⇔\(\left[{}\begin{matrix}a-1\ne0\\a+1\ne0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a\ne1\\a\ne-1\end{matrix}\right.\)
b) A=\(\dfrac{2a^2}{a^2-1}-\dfrac{a}{a+1}+\dfrac{a}{a-1}\) , a≠1, -1
=\(\dfrac{2a^2}{\left(a-1\right)\left(a+1\right)}-\dfrac{a\left(a-1\right)}{\left(a-1\right)\left(a+1\right)}+\dfrac{a\left(a+1\right)}{\left(a-1\right)\left(a+1\right)}\)
=\(\dfrac{2a^2-a\left(a-1\right)+a\left(a+1\right)}{\left(a-1\right)\left(a+1\right)}\)
=\(\dfrac{2a^2-a^2+a+a^2+a}{\left(a-1\right)\left(a+1\right)}\)
=\(\dfrac{2a^2+2a}{\left(a-1\right)\left(a+1\right)}\) =\(\dfrac{2a\left(a+1\right)}{\left(a-1\right)\left(a+1\right)}\) =\(\dfrac{2a}{a-1}\)
vậy A =\(\dfrac{2a}{a-1}\) với a≠1,-1.
c) Có:A= \(\dfrac{2a}{a-1}\) = \(\dfrac{2a-2+2}{a-1}=\dfrac{2\left(a-1\right)+2}{a-1}=2+\dfrac{2}{a-1}\)
Để a∈Z thì a-1 ∈ Z ⇒ (a-1) ∈ Ư(2) =\(\left\{1;-1;2;-2\right\}\)
Ta có bảng sau:
| a-1 | 1 | -1 | 2 | -2 |
| a | 2 | 0 | 3 | -1 |
| Thử lại | TM | TM | TM | ko TM(vì a≠-1 |
Vậy để biểu thức A có giá trị nguyên thì a∈\(\left\{2;0;3\right\}\)
a) ĐKXĐ: \(a\notin\left\{1;-1\right\}\)
b) Ta có: \(A=\dfrac{2a^2}{a^2-1}-\dfrac{a}{a+1}+\dfrac{a}{a-1}\)
\(=\dfrac{2a^2}{\left(a+1\right)\left(a-1\right)}-\dfrac{a\left(a-1\right)}{\left(a+1\right)\left(a-1\right)}+\dfrac{a\left(a+1\right)}{\left(a+1\right)\left(a-1\right)}\)
\(=\dfrac{2a^2-a^2+a+a^2+a}{\left(a+1\right)\left(a-1\right)}\)
\(=\dfrac{2a^2+2a}{\left(a+1\right)\left(a-1\right)}\)
\(=\dfrac{2a\left(a+1\right)}{\left(a+1\right)\left(a-1\right)}\)
\(=\dfrac{2a}{a-1}\)
c) Để A nguyên thì \(2a⋮a-1\)
\(\Leftrightarrow2a-2+2⋮a-1\)
mà \(2a-2⋮a-1\)
nên \(2⋮a-1\)
\(\Leftrightarrow a-1\inƯ\left(2\right)\)
\(\Leftrightarrow a-1\in\left\{1;-1;2;-2\right\}\)
\(\Leftrightarrow a\in\left\{2;0;3;-1\right\}\)
Kết hợp ĐKXĐ, ta được: \(a\in\left\{0;2;3\right\}\)
Vậy: Để A nguyên thì \(a\in\left\{0;2;3\right\}\)

a) Ta có: \(B=\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}-1}\right):\dfrac{a-1}{a-2\sqrt{a}+1}\)
\(=\left(\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}+\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)^2}\)
\(=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\sqrt{a}-1}{\sqrt{a}+1}\)
\(=\dfrac{1}{\sqrt{a}}\)
b) Thay \(a=3-2\sqrt{2}\) vào biểu thức \(B=\dfrac{1}{\sqrt{a}}\), ta được:
\(B=\dfrac{1}{\sqrt{3-2\sqrt{2}}}=\dfrac{1}{\sqrt{2}-1}=\sqrt{2}+1\)
Vậy: Khi \(a=3-2\sqrt{2}\) thì \(B=\sqrt{2}+1\)

\(\left(\frac{a}{a-1}-\frac{1}{a^2-a}\right)=\frac{a^2-1}{a^2-a}=\frac{a+1}{a}\)
ở phàn a+/a thiếu số 1 nhé
\(\frac{1}{a+1}+\frac{2}{a^2-1}=\frac{a-1+2}{a^2-1}=\frac{1}{a-1}\)
=> K =\(\frac{a^2-1}{a}\)
đkxđ: a khác +-1
b, thay vào mà tình
a/ \(K=\left(\frac{a}{a-1}-\frac{1}{a^2-a}\right):\left(\frac{1}{a+1}+\frac{2}{a^2-1}\right)\)
\(=\left(\frac{a}{a-1}-\frac{1}{a\left(a-1\right)}\right):\left(\frac{1}{a+1}+\frac{2}{\left(a-1\right)\left(a+1\right)}\right)\)
\(=\frac{a^2-1}{a\left(a-1\right)}:\frac{a-1+2}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{\left(a-1\right)\left(a+1\right)}{a\left(a-1\right)}.\frac{\left(a-1\right)\left(a+1\right)}{a-1}\)
\(=\frac{a+1}{a}.a+1\)
\(=\frac{\left(a+1\right)^2}{a}\)
b, Thay a=1/2
\(\Rightarrow\frac{\left(\frac{1}{2}+1\right)^2}{\frac{1}{2}}=\frac{\frac{9}{4}}{\frac{1}{2}}=\frac{9}{2}\)