Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I; J lần lượt là trung điểm của SA; SB. Hỏi khẳng định nào sau đây là sai.
A. IJCD là hình thang
B. S A B ∩ I B C = I B .
C. S B D ∩ J C D = J D .
D. I A C ∩ J B D = A O (O là tâm ABCD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Số mặt bên là 4
\(SAB;SAD;SBC;SCD\)
2: Số cạnh đáy là 4
AB,BC,CD,DA
3: SA và BC là hai đường thẳng chéo nhau
4: 4 đỉnh: A,B,C,D
5: Có 7 mặt: \(SAB;SAD;SBC;SCD;SAC;SBD;ABCD\)
6C

Vì CD ⊂ (MCD), CD // AB, AB ⊂ (SAB) nên giao tuyến của (MCD) và (SAB) là đường thẳng qua M và song song với AB, cắt SB tại N là trung điểm của SB. Vậy MN // CD. Hơn nữa MN ≠ CD. Vậy thiết diện là hình thang CNMD.
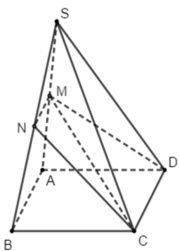
Đáp án C

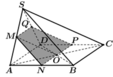
Tham khảo hình vẽ bên.
Gọi P, Q lần lượt là trung điểm của CD, SD. Khi đó thiết diện tạo bởi mặt phẳng (OMN) với hình chóp là hình thang MNPQ. Thật vậy:
![]()
Chọn B.
+ Ta có IJ là đường trung bình của tam giác SAB nên IJ// AB// CD
=> IJCD là hình thang. Do đó A đúng.
+ Ta có I B ⊂ S A B I B ⊂ I B C ⇒ S A B ∩ I B C = I B . Do đó B đúng.
+ Ta có J D ⊂ S B D J D ⊂ J B D ⇒ S B D ∩ J B D = J D . Do đó C đúng.
+ Trong mặt phẳng (IJCD), gọi IC và JD cắt nhau tại M .,
=> giao tuyến của mặt phẳng (IAC) và (JBD) là MO
Do đó D sai.
Chọn D.
chào cậu nha^^