Cho đường thẳng (d): x – 3y = 0, đường thẳng (d’): x – 3y – 10 = 0. Tìm tọa độ vectơ u → có giá vuông góc với đường thằng (d) để (d’) là ảnh của (d) qua T u →
A. 1 ; − 3
B. 2 ; − 6
C. 3 ; − 9
D. Một kết quả khác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Đường thẳng d 2 qua M vuông góc với có vectơ chỉ phương là v → = ( 2 ; − 3 ) .
Do đó phương trình của
d
2
là 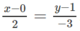 .
.
Gọi M' là giao của d 1 với d 2 thì tọa độ của nó phải thỏa mãn hệ phương trình:
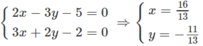
Từ đó suy ra
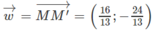

a, Bán kính: \(R=2\sqrt{5}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=20\)
Giao điểm của d và (C) có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}\left(x+1\right)^2+\left(y-2\right)^2=20\\x+3y+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(3y+4\right)^2+\left(y-2\right)^2=20\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10y^2+20y=0\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x=-5\end{matrix}\right.\\\left\{{}\begin{matrix}y=-2\\x=1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}M=\left(0;-5\right)\\N=\left(-2;1\right)\end{matrix}\right.\) là các giao điểm
b, Gọi H là trung điểm AB.
Đường thẳng \(\Delta\) vuông góc với d nên có phương trình dạng: \(3x-y+m=0\left(m\in R\right)\)
Ta có: \(S_{IAB}=\dfrac{1}{2}.R^2.sinAIB=10.sinAIB=5\sqrt{3}\)
\(\Rightarrow sinAIB=\dfrac{\sqrt{3}}{2}\)
Mà tam giác ABC tù nên \(\widehat{AIB}=120^o\)
\(\Rightarrow\widehat{HBI}=30^o\)
Khi đó:
\(IH=d\left(I;\Delta\right)\)
\(\Leftrightarrow R.sinHBI=\dfrac{\left|-3-2+m\right|}{\sqrt{10}}\)
\(\Leftrightarrow2\sqrt{5}.sin30^o=\dfrac{\left|m-5\right|}{\sqrt{10}}\)
\(\Leftrightarrow m=5\pm5\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:3x-y+5+5\sqrt{2}=0\\\Delta:3x-y+5-5\sqrt{2}=0\end{matrix}\right.\)

a, Bán kính: \(R=2\sqrt{545}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=2180\)
Giao điểm của \(\left(C\right);\left(d\right)\) có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}x+3y+5=0\\\left(x+1\right)^2+\left(y-2\right)^2=2180\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-3y-5\\\left(-3y-4\right)^2+\left(y-2\right)^2=2180\end{matrix}\right.\)
\(\Leftrightarrow...\)

1.
\(a,\Leftrightarrow2m-1+m-2=6\Leftrightarrow3m=9\Leftrightarrow m=3\\ b,2x+3y-5=0\Leftrightarrow3y=-2x+5\Leftrightarrow y=-\dfrac{2}{3}x+\dfrac{5}{3}\)
Để \(\left(d\right)\text{//}y=-\dfrac{2}{3}x+\dfrac{5}{3}\Leftrightarrow\left\{{}\begin{matrix}2m-1=-\dfrac{2}{3}\\m-2\ne\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{6}\\m\ne\dfrac{11}{3}\end{matrix}\right.\Leftrightarrow m=\dfrac{1}{6}\)
\(c,x+2y+1=0\Leftrightarrow2y=-x-1\Leftrightarrow y=-\dfrac{1}{2}x-\dfrac{1}{2}\\ \left(d\right)\bot y=-\dfrac{1}{2}x-\dfrac{1}{2}\Leftrightarrow\left(-\dfrac{1}{2}\right)\left(2m-1\right)=-1\\ \Leftrightarrow\dfrac{1}{2}\left(2m-1\right)=1\Leftrightarrow m-\dfrac{1}{2}=1\Leftrightarrow m=\dfrac{3}{2}\)
2.
Gọi điểm cố định đó là \(A\left(x_0;y_0\right)\)
\(\Leftrightarrow y_0=\left(2m-1\right)x_0+m-2\\ \Leftrightarrow2mx_0+m-x_0-2-y_0=0\\ \Leftrightarrow m\left(2x_0+1\right)-\left(x_0+y_0+2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x_0=-1\\x_0+y_0+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-\dfrac{1}{2}\\y_0=-\dfrac{3}{2}\end{matrix}\right.\)

Đáp án B
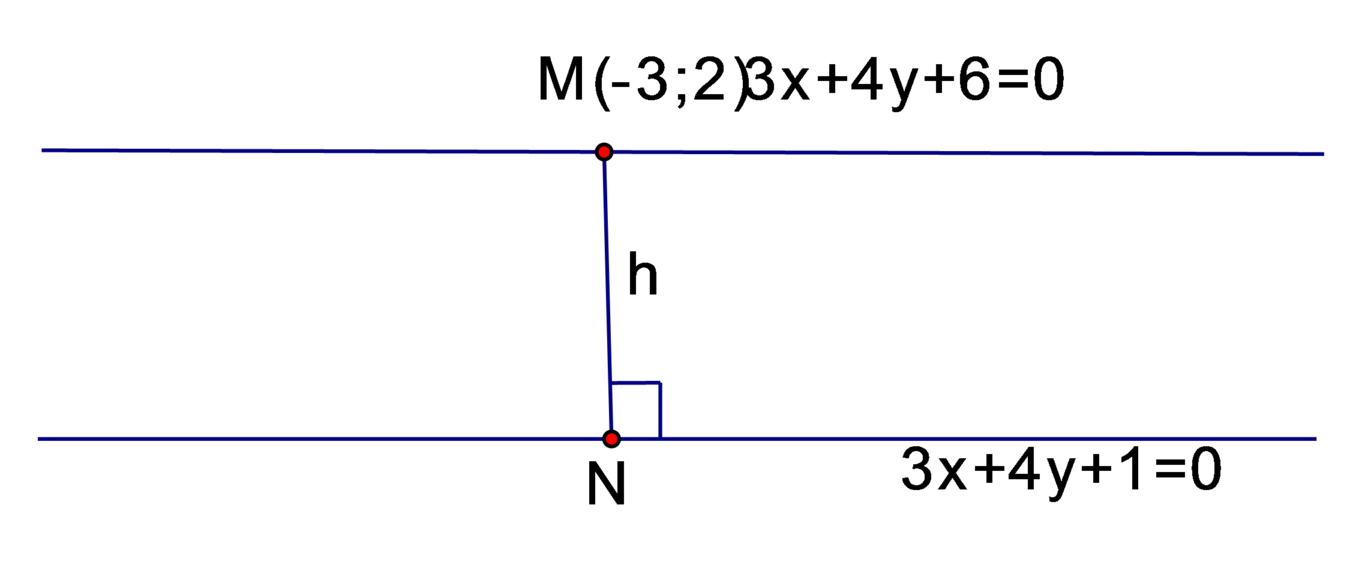
Độ dài véc tơ v → bé nhất đúng bằng khoảng cách h giữa d và d' . h chính là khoảng cách từ M ∈ d tới N ∈ d ' sao cho M N → ⊥ u → 4 ; − 3 trong đó u → là VTCP của cả d và d' .Và khi đó: v → = M N →
Chọn M − 3 ; 2 ∈ d . Ta cần tìm N t ; − 6 − 3 t 4 ∈ d ' sao cho:
M N → t + 3 ; − 14 − 3 t 4 ⊥ u → 4 ; − 3
⇔ 4 t + 12 + 42 + 9 t 4 = 0 ⇔ t = − 18 5
⇒ M N → = − 3 5 ; − 4 5

Chọn D
Đường thẳng (d) có VTPT là (2;3) và VTCP là (3; -2)
Do đường thẳng (d) và ∆ vuông góc với nhau nên đường thẳng ∆ nhận VTCP của đường thẳng (d) làm VTPT.
Do đó đường thẳng ∆ có VTPT là (3; -2) .
Đáp án A
Vectơ pháp tuyến của đường thẳng d là v → (1; –3). Ta có u → = k v → ( k ≠ 0 do d ≠ d ' )
⇔ u → ( k ; − 3 k ) . Áp dụng biểu thức tọa độ, ta có: x ' = k + x y ' = − 3 k + y ( trong đó x’; y’ thỏa mãn phương trình đường thẳng (d’))
=> k + x – 3( –3k + y) – 10 = 0 => x − 3 y + 10 k – 10 = 0 x − 3 y = 0 => k = 1