Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, B C = a 2 . Tính số đo của góc giữa hai đường thẳng AB và SC ta được kết quả
A. 90 °
B. 30 °
C. 60 °
D. 45 °
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 2 2019
Đáp án là B
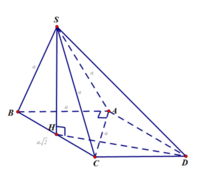
Cách 1. Xác định và tính góc giữa hai đường thẳng.
Tam giác ABC vuông tại A
Do SA=SB=SC nên nếu gọi H là hình chiếu vuông góc của S lên (ABC) thì H là tâm đường tròn ngoại tiếp tam giác ABC mà tam giác ABC vuông tại A nên H là trung điểm của BC.
Dựng hình bình hành ABCD. Khi đó:(AB,SC)=(CD,SC) và CD=AB=a. Tam giác SBC vuông tại S
có SH là đường trùng tuyến nên SH= a 2 2
Tam giác CDH có
theo định lý Cô- Sin ta có
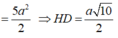
Tam giác SHD vuông tại H nên
Tam giác SCD có:
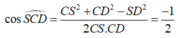
Cách 2. (Hay phù hợp với bài này) Ứng dụng tích vô hướng.
Theo giả thiết có
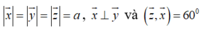
Ta có
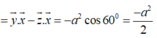
Suy ra:
CM
12 tháng 8 2019
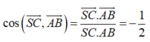
Chọn B.
Cách 1. Xác định và tính góc giữa hai đường thẳng
∆
ABC vuông tại A 
Do SA = SB = SC nên nếu gọi H là hình chiếu vuông góc của S lên (ABC) thì H là tâm đường trong ngoại tiếp tam giác ABC mà ∆ ABC vuông tại A nên H là trung điểm của BC. Dựng hình bình hành ABCD. Khi đó (AB;SC) = (CD;SC) và CD = AB = a
∆
SBC vuông tại S (vì 
có SH là đường trung tuyến nên SH =
a
2
2
theo định lí Cô – Sin ta có
∆ SHD vuông tại H nên
∆
SCD có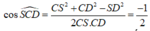 
Cách 2. (Hay phù hợp với bài này) Ứng dụng tích vô hướng
Đặt 
Theo giả thiết ta có: 
Ta có: 
Xét 
Suy ra: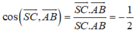 
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2022
Dựng hình vuông ABDC
\(\Rightarrow SA=SB=SC=SD=2\) ; \(CD=AB=2\)
\(CD||AB\Rightarrow\widehat{\left(AB;SC\right)}=\widehat{\left(CD;SC\right)}=\widehat{SCD}\)
Tam giác SCD có \(SC=SD=CD\Rightarrow\Delta SCD\) đều
\(\Rightarrow\widehat{SCD}=60^0\)
CM
10 tháng 5 2018
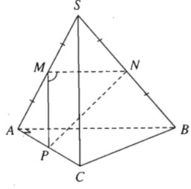
Gọi M, N, P lần lượt là trung điểm của SA, SB. AC. Để tính góc giữa hai đường thẳng SC và AB, ta cần tính ∠NMP.
Ta có:
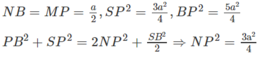
Mặt khác:
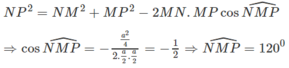
Vậy góc giữa hai đường thẳng SC và AB bằng 60 ο .
CM
27 tháng 9 2017
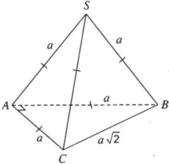
Ta tính côsin của góc giữa hai vectơ S C → và A B → . Ta có
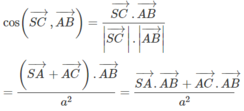
Theo giả thiết ta suy ra hình chóp có các tam giác đều là SAB, SAC và các tam giác vuông là ABC vuông tại A và SBC vuông tại S.
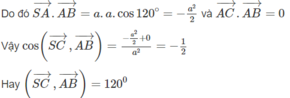
Vậy góc giữa hai vectơ A B → v à S C → bằng 120 o .
Chọn C
* Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABC), theo đầu bài SA=SB=SC và tam giác ABC vuông cân tại A ta có H là trung điểm của BC. Gọi M, N lần lượt là trung điểm của SA, SB ta có: