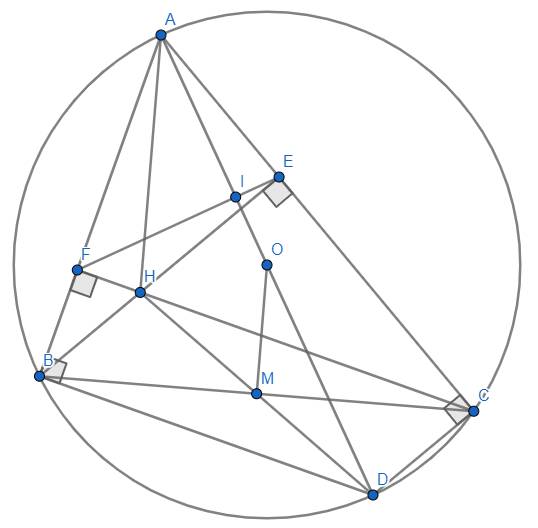
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn 0. Kẻ các đường cao AF và CE của tam giác ABC cắt nhau tại H:
a) Chứng minh tứ giác AEFC nội tiếp đường tròn.
b) Kẻ đường kính AK của đường tròn 0. Chứng minh tam giác ABK đồng dạng với tam giác AFC



tứ giác AECF có góc AEC=AFC là 2 góc kề nhìn cạnh AC nên nt đg tròn
b) ta có : góc ABK =0,5 sđ cung AK=90 độ
xet tam giac ABK và AFC có
góc ABK=góc AFC=90 độ
goc AKB =góc ACF (GÓC NT CHAN CUNG AB)
=>Tam giác ABK đồng dạng vs tam giác AFC(G.G)
Tứ giác AECF có góp AEC=ACF laf2 góc kề nhìn cạnh AC nên nối tiếp đường tròn
B)Ta có:Góc ABK=0,5 sđ cùng AK=90 độ
Xét tam giác ABK