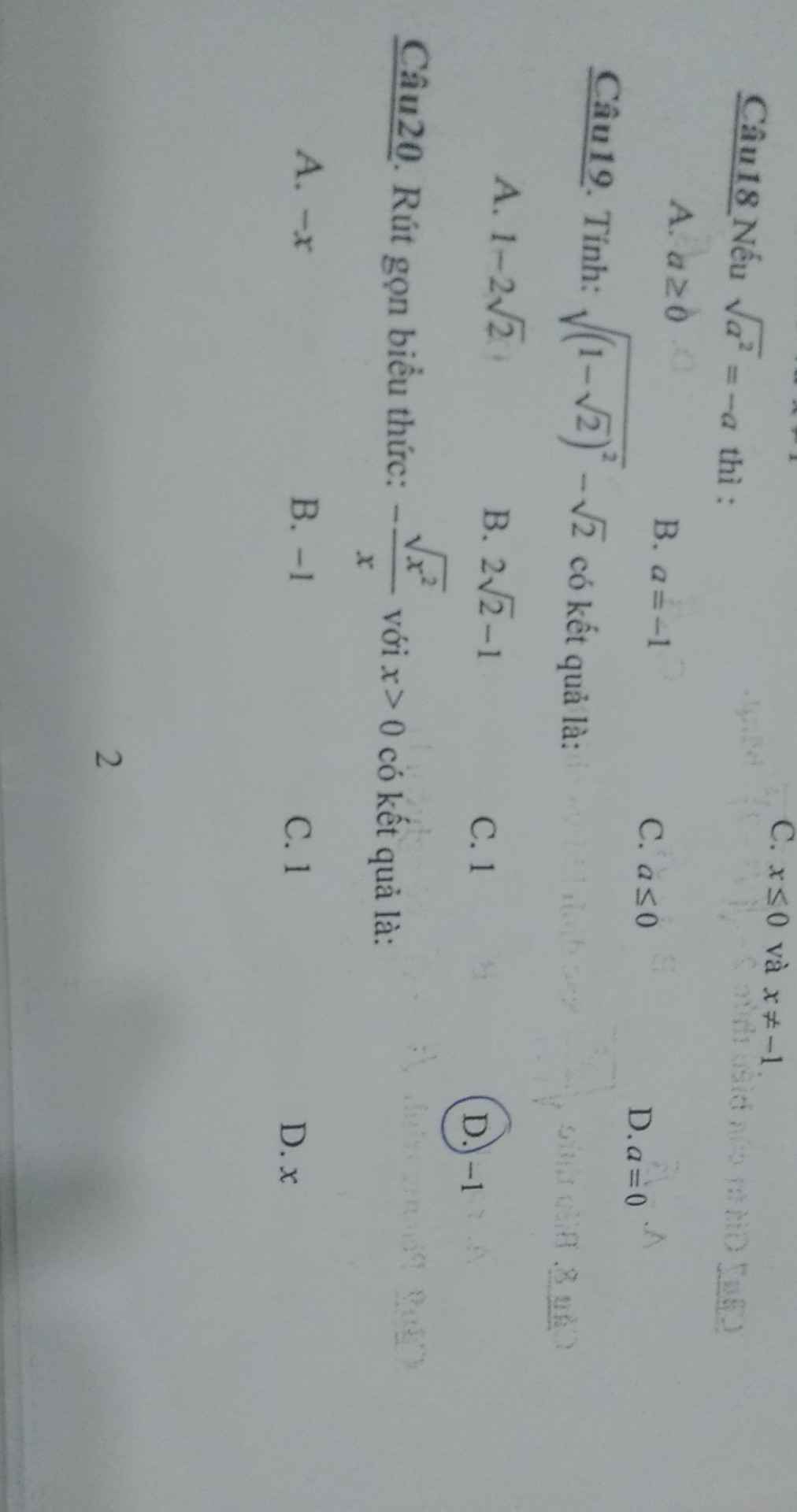Giúp mình những câu chưa khoanh với ạ. Mình cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PH
0
Những câu hỏi liên quan
12 tháng 5 2022
Para 1 - b
Para 2 - a
Para 3 - c
T - F - T - T - NG
1 B
2 A
3 D
4 D
5 A
SB
6 tháng 7 2021
mình làm những bài bn chưa lm nhé
9B
10A
bài 2
have repainted
bàii 3
ride - walikking
swimming
watch
DT
2
29 tháng 8 2021
VII:
1. older than
2. more expensive than
3. more difficult than
4. longer than
5. more modern than
6. younger than
7. more expensive
8. the coldest
9. larger
NT
29 tháng 8 2021
VI.
1. d → strongest
2. b → shorter
3. b → higher
4. d → as
5. d → youngest
6. d → than
VII.
1. older than
2. more expensive than
3. more difficult than
4. longer than
5. more modern
6. the youngest
7. more expensive
8. the coldest
9. larger than
VIII.
1. c
2. c
3. a
4. c
5. b
P
1
PN
1
10 tháng 12 2023
Câu V:
a: Xét ΔABD vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BD;AD^2=DH\cdot DB\)
=>\(\dfrac{AB^2}{AD^2}=\dfrac{BH\cdot BD}{DH\cdot DB}=\dfrac{BH}{DH}\)
=>\(\dfrac{BH}{DH}=\dfrac{CD^2}{BC^2}=\left(\dfrac{CD}{BC}\right)^2=\left(\dfrac{CD}{3CD}\right)^2=\dfrac{1}{9}\)
=>\(DH=9BH\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\)
=>\(9\cdot BH\cdot BH=\left(3\sqrt{10}\right)^2=90\)
=>\(BH^2=10\)
=>\(BH=\sqrt{10}\left(cm\right)\)
=>\(DH=9\sqrt{10}\left(cm\right)\)
\(BD=BH+DH=10\sqrt{10}\left(cm\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BD;AD^2=DH\cdot BD\)
=>\(AB^2=\sqrt{10}\cdot10\sqrt{10}=100;AD^2=9\sqrt{10}\cdot\sqrt{10}=90\)
=>\(AB=10\left(cm\right);AD=3\sqrt{10}\left(cm\right)\)
Chu vi hình chữ nhật ABCD là:
\(C_{ABCD}=\left(AB+AD\right)\cdot2=\left(10+3\sqrt{2}\right)\cdot2\left(cm\right)\)
b: Xét ΔHAD có
M,I lần lượt là trung điểm của HD,HA
=>MI là đường trung bình của ΔHAD
=>MI//AD
Ta có: MI//AD
AB\(\perp\)AD
Do đó: MI\(\perp\)AB
Xét ΔMAB có
MI,AH là các đường cao
MI cắt AH tại I
Do đó: I là trực tâm của ΔMAB
=>BI\(\perp\)AM
NN
1
