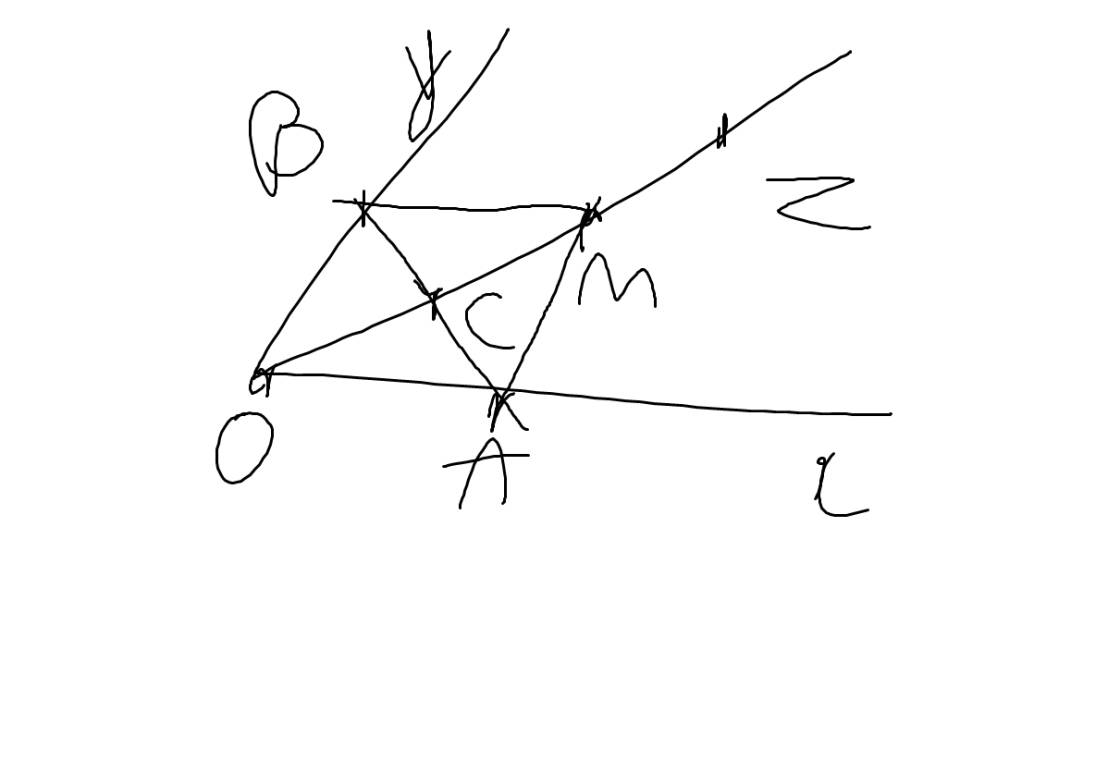
Trên cạnh Ox và Oy của góc xOy lấy hai điểm A và B sao cho OA OB, tia
phân giác góc Oz của góc xOy cắt AB tại C.
a) Chứng minh C là trung điểm của AB và AB vuông góc với OC.
b) Trên tia Cz lấy điểm M sao cho OC CM . Chứng minh: AM OB BM OA // , // .
c) Kẻ MI vuông góc với Oy, MK vuông góc với Ox. So sánh BI và AK.
d) Gọi N là giao điểm của AI và BK. Chứng minh O, N, M thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOAB cân tại O
mà OC là phân giác
nên OC vuông góc AB và C là trung điểm của AB
b: Xét tứ giác OAMB có
C là trung điểm chung của OM và AB
=>OAMB là hình bình hành
=>OA//MB và OB//MA

I don't now
or no I don't
..................
sorry

a: Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>AC=BC
=>C là trung điểm của AB
Ta có: CA=CB
=>C nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OC là đường trung trực của AB
=>CO\(\perp\)AB
b: Xét ΔOAC và ΔMBC có
CO=CM
\(\widehat{OCA}=\widehat{MCB}=90^0\)
CA=CB
Do đó: ΔOAC=ΔMBC
=>\(\widehat{OAC}=\widehat{MBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên OA//BM
Xét ΔCBO vuông tại C và ΔCAM vuông tại C có
CB=CA
CO=CM
Do đó: ΔCBO=ΔCAM
=>\(\widehat{CBO}=\widehat{CAM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BO//AM
Rồi thì h mk nhờ bạn thực hiện như cái mà bạn đã nói đi.
a, Do tam giác OBA cân tại O (vì AO=BO) có OC là tia p/giác (gt) nên:
=> OC cũng là đường cao (1)
và OC cũng là đường trung
tuyến (2)
Từ (1)=> OC vuông góc vs AB (đpcm).
Từ (2)=> BC=AC
Mà C nằm giữa A và B nên:
=> C là trung điểm của AB (đpcm).
b, xét hai tam giác OBC và MAC
OB=OA (gt)
BCO=ACM ( vì đđ)
OC=MC (gt)
=> tam giác OBC bằng tam giác MAC (c-g-c)
=> OBC = MAC (hai góc t/ứng)
Mà OBC và MAC ở vị trí slt nên:
=> OB song song AM (đpcm).
Ý thứ hai của câu b cg cm tương tự
Bạn chỉ cần xét hai tam giác là BCM và ACM rồi suy ra hai góc t/ứng mà hai góc đó nó cg ở vị trí giống như trên.
c, Do tam giác BOM = tam giác AOM (c-g-c) (tự cm)
=> OBM = OAM (3)(hai góc t/ứng).
và BM = AM (hai cạnh t/ứng).
Ta có: IBM + MBO =180 (vì kề bù) (4)
và
KAM + MAO=180 (5) (vì kề bù).
Từ (3); (4) và (5)
=> MBI = MAK
Lại có: hai tam giác MBI và tam giác MAK (ch - gn) (tự cm )
=> BI = AK.
Câu d mk đg mắc việc nên đến sau mk.lm cho nha nhớ theo dõi mk vs nha.