Xin nhờ quý thầy cô và các bạn yêu toán gần xa giúp đỡ với ạ!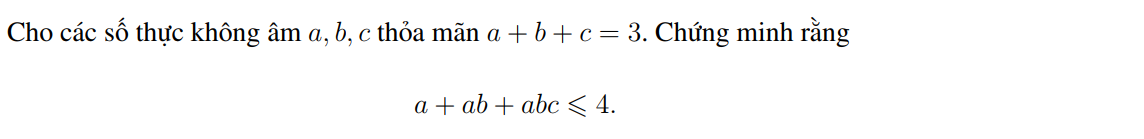
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PK
1

Những câu hỏi liên quan
Áp dụng BĐT cosi dạng \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\cdot\dfrac{1}{4}\ge\dfrac{4}{a+b}\cdot\dfrac{1}{4}\\ \Leftrightarrow\dfrac{1}{a+b}\le\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
\(\Leftrightarrow\dfrac{a}{2a+b+c}=\dfrac{a}{a+b+a+c}\le\dfrac{a}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)\)
Cmtt \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{b}{a+2b+c}\le\dfrac{b}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}\right)\\\dfrac{c}{a+b+2c}\le\dfrac{c}{4}\left(\dfrac{1}{a+c}+\dfrac{1}{b+c}\right)\end{matrix}\right.\)
Cộng VTV 3 BĐT trên:
\(\Leftrightarrow VT\le\dfrac{1}{4}\left(\dfrac{a}{a+b}+\dfrac{a}{a+c}+\dfrac{b}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{a+c}+\dfrac{c}{b+c}\right)\\ \Leftrightarrow VT\le\dfrac{1}{4}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{a+c}{a+c}\right)=\dfrac{1}{4}\cdot3=\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow a=b=c\)
Cám ơn thầy nhiều lắm ạ!