Ghi giúp em cái đk ạ
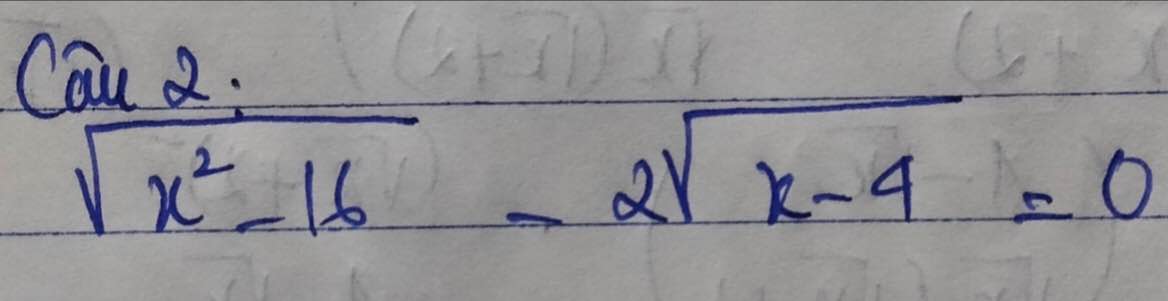
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


để \(\left|8-x\right|=8-x< =>8-x\ge0< =>x\le8\)
\(=>8-x=x^2+x< =>x^2+2x-8=0\)
\(< =>\left(x+1\right)^2-3^2=0< =>\left(x-2\right)\left(x+4\right)=0\)
\(=>\left[{}\begin{matrix}x=2\left(TM\right)\\x=-4\left(TM\right)\end{matrix}\right.\)
*để\(\left|8-x\right|=x-8< =>8-x< 0< =>x>8\)
\(=>x-8=x^2+x< =>x^2=-8\)(vô lí)
vậy x=2 hoặc x=-4

\(đk:\begin{cases}a \ge 0\\1-2\sqrt{a} \ne 0\\\end{cases}\)`<=>` \(\begin{cases}a \ge 0\\a \ne \dfrac14 \\\end{cases}\) $\\$ `C=(a+2sqrta+1-a+4sqrta-4)/(1-2sqrta):sqrta/3=(6sqrta-3)/(1-2sqrta)*3/sqrta=-3*3/sqrta=-9/sqrta`

( Hình em tự vẽ nhé )
+ Ta có: ΔABC = ΔDEF
=> \(\widehat{A}=\widehat{D}=30^o\)
+ Ta có: \(2\widehat{B}=3\widehat{C}\)
=> \(\widehat{B}=\dfrac{3\widehat{C}}{2}\)
+ Xét ΔABC
=> \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(t3g\Delta\right)\)
Mà \(\widehat{A}=30^o;\widehat{B}=\dfrac{3\widehat{C}}{2}\)
=> \(30^o+\dfrac{3\widehat{C}}{2}+\widehat{C}=180^o\)
=> \(\dfrac{3\widehat{C}}{2}+\widehat{C}=150^o\)
\(\Rightarrow\dfrac{3\widehat{C}}{2}+\dfrac{2\widehat{C}}{2}=150^o\)
\(\Rightarrow\dfrac{5\widehat{C}}{2}=150^o\)
\(\Rightarrow5\widehat{C}=75^o\)
\(\Rightarrow\widehat{C}=15^o\)
+ Xét ΔABC
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(t3g\Delta\right)\)
\(\Rightarrow30^o+15^o+\widehat{B}=180^o\)
\(\Rightarrow\widehat{B}=135^o\)
Do chị ko có máy ở đây nên ko chụp hình vẽ đc, em thông cảm nhé😢

sorry , i dont use Wattpad , but you can watch it in youtube :))

Cho cả năm luôn này cj:) Ngữ pháp tiếng Anh lớp 8 cả năm - Hiến thức tiếng Anh lớp 8 học kì 1 + học kì 2 - VnDoc.com

Giải thích cho e hỉu đc ko ạ chứ e bt đáp án mà ko hỉu thì cx như ko í
\(x\ge4\)
\(\sqrt{x^2-16}-2\sqrt{x-4}=0\left(đk:x\ge4\right)\)
\(\Leftrightarrow\sqrt{\left(x-4\right)\left(x+4\right)}-2\sqrt{x-4}=0\)
\(\Leftrightarrow\sqrt{x-4}\left(\sqrt{x+4}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-4}=0\\\sqrt{x+4}=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x+4=4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\)