K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 6 2021
\(đk:\begin{cases}a \ge 0\\1-2\sqrt{a} \ne 0\\\end{cases}\)`<=>` \(\begin{cases}a \ge 0\\a \ne \dfrac14 \\\end{cases}\) $\\$ `C=(a+2sqrta+1-a+4sqrta-4)/(1-2sqrta):sqrta/3=(6sqrta-3)/(1-2sqrta)*3/sqrta=-3*3/sqrta=-9/sqrta`
AH
Akai Haruma
Giáo viên
8 tháng 6 2021
Chỉ với những điều kiện như em nêu thì biểu thức này không rút gọn thêm được.
Còn việc bé hơn hoặc bằng một biểu thức nào khác thì có nhiều. Tốt nhất em nên nêu cụ thể đề để được hỗ trợ tốt hơn.
26 tháng 6 2021
`D=(a+4sqrta+4)/(sqrta+2)+(4-a)/(sqrta-2)`
`=(sqrta+2)^2/(sqrta+2)+((2-sqrta)(2+sqrta))/(sqrta-2)`
`=sqrta+2-(2+sqrta)`
`=0`
TG
26 tháng 6 2021
ĐK: a ≥ 0; a khác 4
\(D=\dfrac{a+\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{\sqrt{a}-2}\)
\(=\dfrac{a+\sqrt{a}+4}{\sqrt{a}+2}-\left(2+\sqrt{a}\right)\)
\(=\dfrac{\left(a+\sqrt{a}+4\right)-\left(2+\sqrt{a}\right)^2}{\sqrt{a}+2}=\dfrac{a+\sqrt{a}+4-\left(4+4\sqrt{a}+a\right)}{\sqrt{a}+2}=\dfrac{a+\sqrt{a}+4-4-4\sqrt{a}-a}{\sqrt{a}+2}=-\dfrac{3}{\sqrt{a}}\)
14 tháng 11 2021
Vì \(\widehat{BEC}=\widehat{BKC}=90^0\)(góc nt chắn nửa đg tròn) nên \(HK\perp MC;ME\perp HC\)
Xét tam giác HMC có 2 đường cao HK,ME (cm trên) cắt nhau tại B nên B là trực tâm
Do đó BC⊥MH
NA
2
Y
17 tháng 1 2023
\(c,\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{1}{y+1}=3\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x-2}+\dfrac{2}{y+1}=6\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{y+1}+\dfrac{3}{y+1}=5\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{y+1}=5\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y+1=1\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=0\left(2\right)\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\left(1\right)\end{matrix}\right.\)
Thay \(\left(2\right)\) vào \(\left(1\right)\) :
\(\dfrac{4}{x-2}-\dfrac{3}{0+1}=1\)
\(\Rightarrow\dfrac{4}{x-2}-3=1\)
\(\Rightarrow\dfrac{4}{x-2}=4\)
\(\Rightarrow x-2=1\)
\(\Rightarrow x=3\)
Vậy hệ phương trình có nghiệm duy nhất \(\left(x;y\right)=\left(3;0\right)\)
17 tháng 1 2023
c: =>4/x-2+2/y+1=6 và 4/x-2-3/y+1=1
=>5/y+1=5 và 2/x-2+1/y+1=3
=>y+1=1 và 2/x-2+1=3
=>y=0 và x-2=1
=>x=3 và y=0
24 tháng 4 2023
a: góc ABM=1/2*120=60 độ
b: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
c: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM
mà OA=OM
nên OC là trung trực của AM
=>OC vuông góc AM
góc AMB=1/2*180=90 độ
=>MB vuông góc AM
=>MB//OC
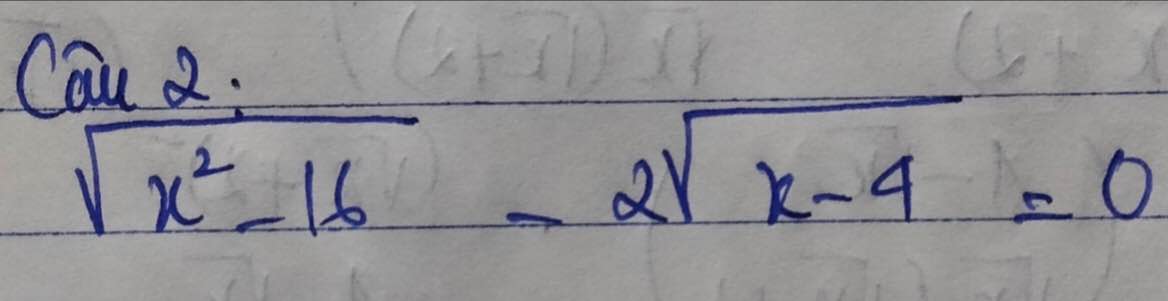
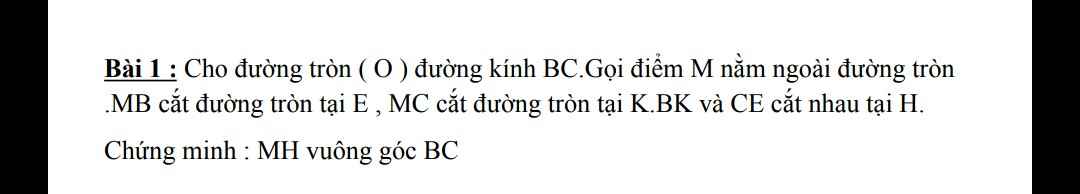
\(x\ge4\)
\(\sqrt{x^2-16}-2\sqrt{x-4}=0\left(đk:x\ge4\right)\)
\(\Leftrightarrow\sqrt{\left(x-4\right)\left(x+4\right)}-2\sqrt{x-4}=0\)
\(\Leftrightarrow\sqrt{x-4}\left(\sqrt{x+4}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-4}=0\\\sqrt{x+4}=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x+4=4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\)