Cho tam giác ABC có: \(\widehat{B}=30\), \(\widehat{C}=15\)AM là đường trung tuyến. Tính số đo góc AMB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Góc AM?? Mình tính luôn ^AMB và ^AMC nhé !
Xét \(\Delta ABC\)có \(\widehat{BAC}+\widehat{B}+\widehat{C}=180^o\)(theo định lý tổng 3 góc trong của 1 tam giác)
\(\Rightarrow\widehat{BAC}+30^o+15^o=180^o\)
\(\Rightarrow\widehat{BAC}=135^o\)
Vì AM là đường trung tuyến của \(\widehat{BAC}\)
\(\Rightarrow\widehat{MAB}=\widehat{MAC}=\frac{\widehat{BAC}}{2}=\frac{135^o}{2}=67,5^o\)
Xét \(\Delta AMB\)có : \(\widehat{MAB}+\widehat{B}+\widehat{AMB}=180^o\)(đ/lý tổng 3 góc trong của 1 tam giác)
\(\Rightarrow67,5^o+30^o+\widehat{AMB}=180^o\)
\(\Rightarrow\widehat{AMB}=82,5^o\)
\(\Rightarrow\widehat{AMC}=180^o-\widehat{AMB}=180^o-82,5^o=97,5^o\)(Vì \(\widehat{AMB}+\widehat{AMC}=180^o\))
Trên mặt phẳng bờ BC chưa A lấy điểm N sao cho \(\Delta\)NCM đều
=> ^CMN = 60 độ
=> ^NMB = 120 độ
Mà NM = MC = BM
=> \(\Delta\)NMB cân tại tại B => ^NBM = 30 độ=> ^CBN = 30 độ mà ^CBA = 30 độ
=> M; A; N thẳng hàng
Xét \(\Delta\)CBN có: ^NCB = 60 độ ; ^CBN = 30 độ
=> ^CNB = 90 độ
=> ^CNA = 90 độ
mà ^ACN = ^MCN - ^MCA = 45 độ
=> \(\Delta\)NCA vuông cân tại N
=> NC = NA mà NC = NM
=> NA = NM => \(\Delta\)NAM cân tại N có: ^MNA = 30 độ => ^NMA = ^NAM = ( 180 - 30 ) : 2 = 75 độ
=> ^CAM = ^NAM - ^NAC = 75 - 45 = 30 độ
=> ^NAB = 180 - 30 - 15 - 30 = 105 độ

Tham khảo:
a) Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.10}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}\)
\( \Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }\), tam giác ABC có góc C tù.
b)
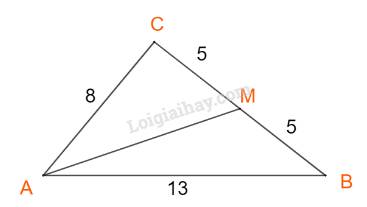
+) Áp dụng định lí cosin trong tam giác ACM, ta có:
\(\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}\)
+) Ta có: \(p = \frac{{8 + 10 + 13}}{2} = 15,5\).
Áp dụng công thức heron, ta có: \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40\)
+) Áp dụng định lí sin, ta có:
\(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5\)
c)

Ta có: \(\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }\); \(CD = AC = 8\)
Áp dụng định lí cosin trong tam giác BCD, ta có:
\(\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}\)



Tham khảo:
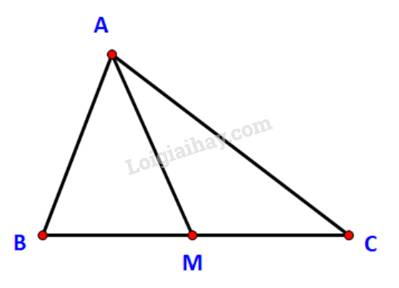
a) Ta có: \(\widehat {AMB} + \widehat {AMC} = {180^o}\)
\( \Rightarrow \cos \widehat {AMB} = - \cos \widehat {AMC}\)
Hay \(\cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
b) Áp dụng định lí cos trong tam giác AMB ta có:
\(\begin{array}{l}A{B^2} = M{A^2} + M{B^2} - 2MA.MB\;\cos \widehat {AMB}\\ \Leftrightarrow M{A^2} + M{B^2} - A{B^2} = 2MA.MB\;\cos \widehat {AMB}\;\;(1)\end{array}\)
Tương tự, Áp dụng định lí cos trong tam giác AMB ta được:
\(\begin{array}{l}A{C^2} = M{A^2} + M{C^2} - 2MA.MC\;\cos \widehat {AMC}\\ \Leftrightarrow M{A^2} + M{C^2} - A{C^2} = 2MA.MC\;\cos \widehat {AMC}\;\;(2)\end{array}\)
c) Từ (1), suy ra \(M{A^2} = A{B^2} - M{B^2} + 2MA.MB\;\cos \widehat {AMB}\;\)
Từ (2), suy ra \(M{A^2} = A{C^2} - M{C^2} + 2MA.MC\;\cos \widehat {AMC}\;\)
Cộng vế với vế ta được:
\(2M{A^2} = \left( {A{B^2} - M{B^2} + 2MA.MB\;\cos \widehat {AMB}} \right)\; + \left( {A{C^2} - M{C^2} + 2MA.MC\;\cos \widehat {AMC}} \right)\;\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - M{B^2} - M{C^2} + 2MA.MB\;\cos \widehat {AMB} + 2MA.MC\;\cos \widehat {AMC}\)
Mà: \(MB = MC = \frac{{BC}}{2}\) (do AM là trung tuyến)
\( \Rightarrow 2M{A^2} = A{B^2} + A{C^2} - {\left( {\frac{{BC}}{2}} \right)^2} - {\left( {\frac{{BC}}{2}} \right)^2} + 2MA.MB\;\cos \widehat {AMB} + 2MA.MB\;\cos \widehat {AMC}\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - 2.{\left( {\frac{{BC}}{2}} \right)^2} + 2MA.MB\;\left( {\cos \widehat {AMB} + \;\cos \widehat {AMC}} \right)\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - {\frac{{BC}}{2}^2}\)
\(\begin{array}{l} \Leftrightarrow M{A^2} = \frac{{A{B^2} + A{C^2} - {{\frac{{BC}}{2}}^2}}}{2}\\ \Leftrightarrow M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\end{array}\) (đpcm)
Cách 2:
Theo ý a, ta có: \(\cos \widehat {AMC} = - \cos \widehat {AMB}\)
Từ đẳng thức (1): suy ra \(\cos \widehat {AMB} = \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}\)
\( \Rightarrow \cos \widehat {AMC} = - \cos \widehat {AMB} = - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}\)
Thế \(\cos \widehat {AMC}\)vào biểu thức (2), ta được:
\(M{A^2} + M{C^2} - A{C^2} = 2MA.MC.\left( { - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}} \right)\)
Lại có: \(MB = MC = \frac{{BC}}{2}\) (do AM là trung tuyến)
\(\begin{array}{l} \Rightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} = 2MA.MB.\left( { - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}} \right)\\ \Leftrightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} = - \left( {M{A^2} + M{B^2} - A{B^2}} \right)\\ \Leftrightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} + M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{B^2} = 0\\ \Leftrightarrow 2M{A^2} - A{B^2} - A{C^2} + {\frac{{BC}}{2}^2} = 0\\ \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - {\frac{{BC}}{2}^2}\\ \Leftrightarrow M{A^2} = \frac{{A{B^2} + A{C^2} - {{\frac{{BC}}{2}}^2}}}{2}\\ \Leftrightarrow M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\end{array}\)