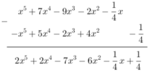cho đa thức f(x) và g(x)biết f(x)+g(x)=6x4 -3x2 -5 và f(x) g(x)= 4x4 -6x3 +7x2 + 8x-9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 4 2023
`a,`
`F(x)=4x^4-2+2x^3+2x^4-5x+4x^3-9`
`F(x)=(2x^4+4x^4)+(2x^3+4x^3)-5x+(-2-9)`
`F(x)=6x^4+6x^3-5x-11`
`b,`
`K(x)=F(x)+G(x)`
`K(x)=(6x^4+6x^3-5x-11)+(6x^4+6x^3-x^2-5x-27)`
`K(x)=6x^4+6x^3-5x-11+6x^4+6x^3-x^2-5x-27`
`K(x)=(6x^4+6x^4)+(6x^3+6x^3)-x^2+(-5x-5x)+(-11-27)`
`K(x)=12x^4+12x^3-x^2-10x-38`
`c,`
`H(x)=F(x)-G(x)`
`H(x)=(6x^4+6x^3-5x-11)-(6x^4+6x^3-x^2-5x-27)`
`H(x)=6x^4+6x^3-5x-11-6x^4-6x^3+x^2+5x+27`
`H(x)=(6x^4-6x^4)+(6x^3-6x^3)+x^2+(-5x+5x)+(-11+27)`
`H(x)=x^2+16`
Đặt `x^2+16=0`
Ta có: \(x^2\ge0\text{ }\forall\text{ }x\)
`->`\(x^2+16\ge16>0\text{ }\forall\text{ }x\)
`->` Đa thức `H(x)` vô nghiệm.
H
13 tháng 4 2023
Bài 1
Gợi ý bạn làm : Bạn thay \(x=-4;x=-3;x=0;x=1\) vào \(f\left(x\right);g\left(x\right)\)
\(\Rightarrow\) Nếu kết quả ra giống nhau thì là nghiệm , ra khác nhau thì không là nghiệm
VD : Thay \(x=-4\) vào \(f\left(x\right)\) và \(g\left(x\right)\)
\(f\left(-4\right)=4.\left(-4\right)^4-5\left(-4\right)^3+3.\left(-4\right)+2=1334\)
\(g\left(x\right)=-4.\left(-4\right)^4+5\left(-4\right)^3+7=-1337\)
Ra hai kết quả khác nhau
\(\Rightarrow x=-4\) không là nghiệm
Bài 2
\(f\left(x\right)-g\left(x\right)=\left(-x^5+3x^2+4x+8\right)-\left(-x^5-3x^2+4x+2\right)\\ =-x^5+3x^2+4x+8+x^5+3x^2-4x-2\\ =\left(-x^5+x^5\right)+\left(3x^2+3x^2\right)+\left(4x-4x\right)+\left(8-2\right)\\ =6x^2+6\\ =x^2+1\\ =x^2+2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}\\ =\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)
\(\Rightarrow\) phương trình vô nghiệm
24 tháng 6 2021
a)\(f\left(x\right)=2x^2-x-3+5=\left(x+1\right)\left(2x-3\right)+5\)
Để \(f\left(x\right)⋮g\left(x\right)\Leftrightarrow\left(x+1\right)\left(2x-3\right)+5⋮\left(x+1\right)\)
\(\Leftrightarrow5⋮\left(x+1\right)\)
mà \(x+1\in Z\Rightarrow x+1\in U\left(5\right)=\left\{-1;1;5;-5\right\}\)
\(\Leftrightarrow x\in\left\{-2;0;4;-6\right\}\)
Vậy...
b) \(f\left(x\right)=3x^2-4x+6=\left(3x^2-4x+1\right)+5=\left(3x-1\right)\left(x-1\right)+5\)
Để \(f\left(x\right)⋮g\left(x\right)\Leftrightarrow\left(3x-1\right)\left(x-1\right)+5⋮\left(3x-1\right)\)
\(\Leftrightarrow5⋮\left(3x-1\right)\) mà \(3x-1\in Z\Rightarrow3x-1\in U\left(5\right)=\left\{-1;1;5;-5\right\}\)
\(\Leftrightarrow x\in\left\{0;\dfrac{2}{3};2;-\dfrac{4}{3}\right\}\) mà x nguyên\(\Rightarrow x\in\left\{0;2\right\}\)
Vậy...
c)\(f\left(x\right)=\left(-2x^3-7x^2-5x+2\right)+3\)\(=\left(-2x^3-4x^2-3x^2-6x+x+2\right)+3\)\(=\left[-2x^2\left(x+2\right)-3x\left(x+2\right)+\left(x+2\right)\right]+3\)
\(=\left(x+2\right)\left(-2x^2-3x+1\right)+3\)
Làm tương tự như trên \(\Rightarrow x+2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Leftrightarrow x\in\left\{-5;-3;-1;1\right\}\)
Vậy...
d)\(f\left(x\right)=x^3-3x^2-4x+3=x\left(x^2-3x-4\right)+3=x\left(x+1\right)\left(x-4\right)+3\)
Làm tương tự như trên \(\Rightarrow x+1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Rightarrow x\in\left\{-4;-2;0;2\right\}\)
Vậy...
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(f\left(x\right)=x^3-x+7\)
\(g\left(x\right)=-x^3+8x-14\)
\(\Rightarrow f\left(x\right)+g\left(x\right)=7x-7\)
Nghiệm của đa thức \(f\left(x\right)+g\left(x\right)=0\Rightarrow7x-7=0\)
\(\Rightarrow x=1\)
15 tháng 8 2021
a: \(F\left(x\right)=x^5-3x^2+x^3-x^2-2x+5\)
\(=x^5+x^3-4x^2-2x+5\)
\(G\left(x\right)=x^5-x^4+x^2-3x+x^2+1\)
\(=x^5-x^4+2x^2-3x+1\)
b: Ta có: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^5+x^3-4x^2-2x+5+x^5-x^4+2x^2-3x+1\)
\(=2x^5-x^4+x^3-2x^2-5x+6\)
CM
6 tháng 9 2018
b. Ta có f(x) + 2g(x)
= x3 - 2x2 + 2x- 5 + 2(-x3 + 3x2 - 2x + 4)
= x3 - 2x2 + 2x - 5 + (-2x3) + 6x2 - 4x + 8
=-x3 + 4x2 - 2x + 3 (0.5 điểm)
2f(x) - g(x) = x3 - 2x2 + 2x- 5 - 2(-x3+ 3x2 - 2x + 4)
= x3 - 2x2 + 2x - 5 + 2x3 - 6x2 + 4x - 8
= 3x3 - 8x2 + 6x - 13 (0.5 điểm)
CM
31 tháng 3 2019
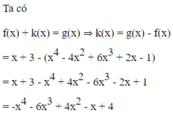
Nhận thấy số hạng có lũy thừa cao nhất của biến là - x 4 nên hệ số cao nhất là -1
Chọn đáp án A
CM
22 tháng 1 2017
Ta có f(x) + g(x) = 4x - 1. Khi đó nghiệm của đa thức tổng là x = 1/4. Chọn C
6 tháng 8 2015
=> 2 f(x) = 6x^4 - 3x^2 - 5 + 4x^4 - 6x^3 + 7x^2 + 8x - 9
= 10x^4 - 6x^3 + 4x^2 + 8x - 14
=> 2.f ( x ) = 2 ( 5x^4 - 3x^3 + 2x^2 + 4x - 7 )
=> ( fx) = 5x^4 - 3x^3 + 2x^2 + 4x - 7
g(x) tự tìm
MT
6 tháng 8 2015
ta có:
f(x) + g(x) = 6x^4 - 3x^2 - 5
f(x) - g(x) = 4x^4 - 6x^3 + 7x^2 + 8x - 9
công hai vế lại với nhau ta được:
f(x)+g(x)+f(x)-g(x)=6x^4 - 3x^2 - 5 + 4x^4 - 6x^3 + 7x^2 + 8x - 9
=>2f(x)=6x4+4x4-6x3-3x2+7x2+8x-5-9
2f(x)=10x4-6x3+4x2+8x-14
2f(x)=2.(5x4-3x3+2x2+4x-7)
=>f(x)=5x4-3x3+2x2+4x-7
=>g(x)=6x^4 - 3x^2 - 5 -(5x4-3x3+2x2+4x-7)
=6x4-3x2-5-5x4+3x3-2x2-4x+7
=6x4-5x4+3x3-3x2-2x2-4x-5+7
=x4+3x3-5x2-4x+2
CM
3 tháng 7 2018
* Ta có:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
= x5 – (3x2 – x2) + 7x4 – 9x3 -1/4.x
= x5 – 2x2 + 7x4 – 9x3 -1/4.x
= x5 + 7x4 – 9x3 – 2x2 - 1/4
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
= 5x4 –x5+ (x2 + 3x2) – 2x3 – 1/4
= 5x4 – x5 + 4x2 – 2x3 – 1/4
= -x5 + 5x4 – 2x3 + 4x2 - 1/4
* f(x) + g(x)
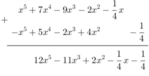
* f(x) - g(x)
