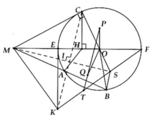
Từ điểm M nằm ngoài đường tròn (O) vẽ 2 tiếp tuyến MP và MQ với đường tròn (P và Q là 2 tiếp điểm). Trên nửa mặt phẳng bờ là đường thẳng OM chứa điểm P vẽ cát tuyến MAB (A nằm giữa M và B), gọi I là trung điểm của AB.
a) Chứng minh 5 điểm M, P, O, I, Q cùng thuộc một đường tròn.
b) PQ cắt AB tại E. Chứng minh rằng MP2 = ME. MI
c) Qua A kẻ đường thẳng song song với MP cắt PQ, PB lần lượt tại H và K. Chứng minh rằng KB = 2. HI


Ta có : MP = MQ (tính chất tiếp tuyến)
=> \(\Delta\) MPQ là tam giác cân
=> ^MPQ = ^MQP
mà ^MQP = ^MIP (2 góc nội tiếp cùng chắng cung MP)
=> ^MPQ = ^MIP => ^MPE = ^MIP
Xét \(\Delta\) MPE và \(\Delta\) MIP ta có :
M: góc chung
^MPE = ^MIP (cmt)
=> \(\Delta\)MPE đồng dạng \(\Delta\) MIP (g.g)
=> \(\frac{MP}{MI}=\frac{ME}{MB}\)
=> đpcm