Bài 1: tìm a để f(x) liên tục trên [-3; +∞)
\(f\left(x\right)=\left\{{}\begin{matrix}\frac{\sqrt{x+3}-\sqrt[3]{3x+5}}{x-1}\left(x\ne1\right)\\ax+1\left(x=1\right)\end{matrix}\right.\)
Bài 2: Chứng minh các phương trình sau luôn có nghiêm với mọi m
a. \(m\left(x-1\right)^3\left(x+2\right)+2x+3=0\)
b. \(m\sin^3x-m\cos x=0\)

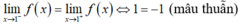

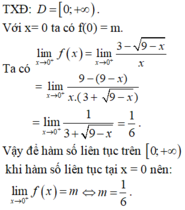
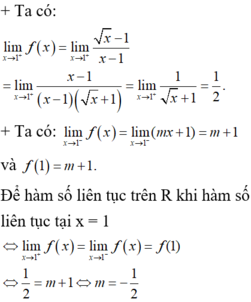
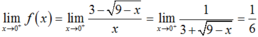 .
.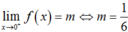 .
.
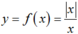 liên tục tại x = 1.
liên tục tại x = 1.
Bài 1:
\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\frac{\sqrt{x+3}-2+2-\sqrt[3]{3x+5}}{x-1}=\lim\limits_{x\rightarrow1}\frac{\frac{x-1}{\sqrt{x+3}+2}-\frac{3\left(x-1\right)}{4+2\sqrt[3]{3x+5}+\sqrt[3]{\left(3x+5\right)^2}}}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\left(\frac{1}{\sqrt{x+3}+2}-\frac{3}{4+2\sqrt[3]{3x+5}+\sqrt[3]{\left(3x+5\right)^2}}\right)=0\)
\(f\left(1\right)=a+1\)
Để hàm số liên tục trên \([-3;+\infty)\Leftrightarrow\) hàm số liên tục tại \(x=1\)
\(\Leftrightarrow\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\Rightarrow a+1=0\Rightarrow a=-1\)
Bài 2:
Các hàm số đã cho đều liên tục trên R nên liên tục trên từng khoảng bất kì
a/ Xét \(f\left(x\right)=m\left(x-1\right)^3\left(x+2\right)+2x+3\)
\(f\left(-2\right)=-1\) ; \(f\left(1\right)=5\)
\(\Rightarrow f\left(-2\right).f\left(1\right)< 0;\forall m\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\) với mọi m
b/ \(m\left(sin^3x-cosx\right)=0\)
Nếu \(m=0\) pt có vô số nghiệm (thỏa mãn)
Nếu \(m\ne0\Leftrightarrow f\left(x\right)=sin^3x-cosx=0\)
\(f\left(0\right)=-1\) ; \(f\left(\frac{\pi}{2}\right)=1\)
\(\Rightarrow f\left(0\right).f\left(\frac{\pi}{2}\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\frac{\pi}{2}\right)\)
Phương trình luôn có nghiệm với mọi m