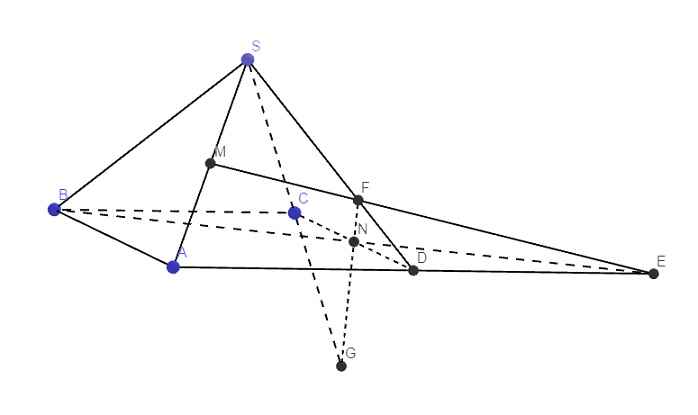
Bài 2: Cho hình chóp S.ABCD đáy là hình bình hànhtâm Gọi M, N, Plần lượt là trung điểm AB, CD, SA
a)Tìm giao tuyến của (MNP ) và (SAD)
b)Tìm giao tuyến của (PBN) và (SAD)
c)Tìm giao điểm của SDvà (PBN)
d)Chứng minh PM///(SBC) và PN//(SBC)
e)Tìm thiết diện của (MNP) với S.ABCD