cho tam giác ABC có AB= 9 cm , AC = 11 cm . kẻ đường cao AH . Biết BH=26cm . Tính CH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
2
D
29 tháng 4 2020
H B C A 9cm 12cm 6cm
Áp dụng đl pitago cho tg BAH vuông tại H có :
BH^2 + AH^2 = AB^2
<=> AH^2 = AB^2 - BH^2 = 9^2 - 6^2
<=> AH^2 = 81 - 36 = 45
<=> AH = \(\sqrt{45}\)
Áp dụng đl pitago cho tam giác ACH vuông tại H có :
AC^2 = AH^2 + CH^2
<=> CH^2 = AC^2 - AH^2
<=> CH^2 = 12^2 - \(\sqrt{45}\) ^2
<=> CH^2 = 144 - 45 = 99
<=> CH = \(\sqrt{99}\)
Vậy ...
NT
3
7 tháng 2 2019
Đề thế này thì tính ra âm à , cạnh góc vuông sao lơn hơn cạnh huyền trời ............
~ xem lại đề nha
~ học tốt!~
PT
1
CM
11 tháng 1 2017
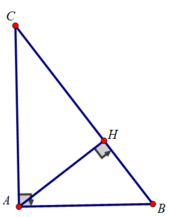
b) Xét tam giác ABC vuông tại A có AH là đường cao nên ta có:
A B 2 = BH.BC
⇒
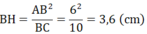
A C 2 = CH.BC
⇒
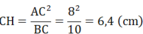
AH.BC = AB.AC
⇒
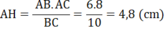
Vậy AH = 4,8 cm; BH = 3,6 cm; CH = 6,4 cm
19 tháng 3 2020
A B C H 8cm 32cm ??? Chỉ mag TC minh họa
AD định lí Py ta go
\(AB^2=AH^2+BH^2=AH^2+8^2=AH^2+64\)
\(\Rightarrow AB=AH^2+64\)
Thực hiện tiếp vs AC
10 tháng 8 2021
a,
pytago trong tam giác ABH
\(=>AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4,5^2}=7,5cm\)
dễ dàng chứng minh \(\Delta AHB\sim\Delta CAB\left(g.g\right)=>\dfrac{AH}{AC}=\dfrac{HB}{AB}=>AC=10cm\)
pytago cho tam giác ABC
\(=>BC=\sqrt{AB^2+AC^2}=12,5cm\)
\(=>HC=BC-HB=8cm\)
b, pytago cho tam giác AHB
\(=>AH=\sqrt{AB^2-BH^2}=3\sqrt{3}cm\)
rồi tính AC , CH làm tương tự bài trên
N
2
12 tháng 9 2021
Ta có: BC=BH+CH
nên BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
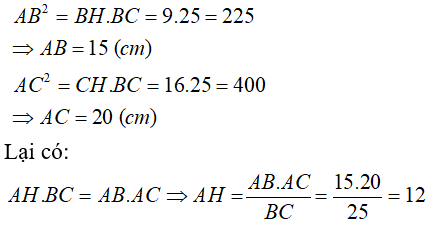
Đề sai bn ơi
Học tốt