Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng PTG: \(AB=\sqrt{BC^2-AC^2}=6\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=3,6\left(cm\right)\\CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\AH=\sqrt{3,6\cdot6,4}=4,8\left(cm\right)\end{matrix}\right.\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Leftrightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx90^0-53^0=37^0\)

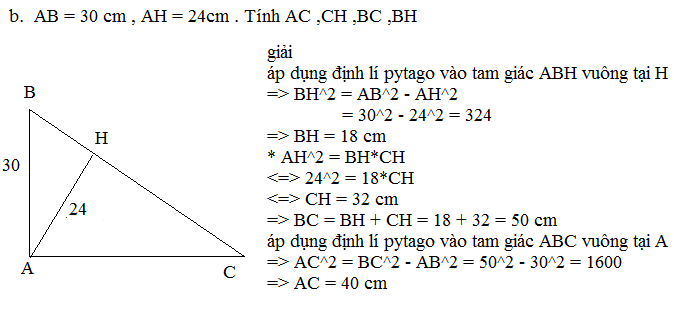
tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{8^2}{10}=6,4\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
b) Kẻ HE,HF vuông góc với AB,AC chớ,chứ ko có điểm I
Vì \(\angle HEA=\angle HFA=\angle EAF=90\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow EF=AH\)
tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow EA.EB=EH^2\)
tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow FA.FC=HF^2\Rightarrow EA.EB+FA.FC=EH^2+FH^2=EF^2=AH^2\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=HB.HC\Rightarrow HB.HC=EA.EB+FA.FC\)

A B C 6 10 H D M N
a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AC^2=100-36=64\Leftrightarrow AC=8\)cm
* Áp dụng hệ thức :
\(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{36}{10}=\frac{18}{5}\)cm
* Áp dụng hệ thức :
\(AH^2=CH.BH\)mà \(BC-BH=CH\Rightarrow CH=10-\frac{18}{5}=\frac{32}{5}\)cm
\(\Rightarrow AH^2=\frac{32}{5}.\frac{18}{5}=\frac{576}{25}\Rightarrow AH=\frac{24}{5}\)cm
Chu vi tam giác ABC là : \(P_{ABC}=AB+AC+BC=6+10+8=24\)cm
Diện tích tam giác ABC là : \(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}.6.8=24\)cm2
b, Ta có AD là phân giác nên : \(\frac{AB}{BC}=\frac{BD}{CD}\)( t/c )
\(\Rightarrow\frac{CD}{BC}=\frac{BD}{AB}\)( tỉ lệ thức )
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{CD}{BC}=\frac{BD}{AB}=\frac{CD+BD}{AB+BC}=\frac{BC}{16}=\frac{1}{2}\)
\(\Rightarrow\frac{BD}{6}=\frac{1}{2}\Rightarrow BD=3\)cm
\(\Rightarrow HD=BH-BD=\frac{18}{5}-3=\frac{3}{5}\)cm
Áp dụng định lí Pytago cho tam giác ADH vuông tại H ta có :
\(AD^2=HD^2+AH^2=\frac{9}{25}+\frac{576}{25}=\frac{585}{25}\Rightarrow AD=\frac{3\sqrt{65}}{5}\)cm

\(AC=\sqrt{BC^2-AB^2}=6\left(cm\right)\left(pytago\right)\)
Áp dụng HTL tam giác:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\CH=\dfrac{AC^2}{BC}=3,6\left(cm\right)\\AH=\sqrt{BH\cdot HC}=4,8\left(cm\right)\end{matrix}\right.\)

\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\\CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\BH=\dfrac{AB^2}{BC}=3,6\left(cm\right)\end{matrix}\right.\)
Áp dụng PTG ta có: \(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{6^2+8^2}=10\)
Áp dụng HTL ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{6.8}{10}=4,8\)
Áp dụng HTL ta có:\(BH.BC=AB^2\Rightarrow BC=\dfrac{6^2}{10}=3,6\)
Áp dụng HTL ta có:\(CH.BC=AC^2\Rightarrow BC=\dfrac{8^2}{10}=6,4\)

a/ Ta có: + AB2 + AC2 = 62 + 82 = 100
+ BC2 = 102 = 100
=> AB2 + AC2 = BC2 = 100
=> tam giác ABC vuông tại A theo định lí pytago
b/ 4 ý này trong sách hình học 9 có CM nha bạn
c/ AH.BC = AB.AC
=> AH = \(\frac{AB.AC}{BC}=\frac{6.8}{10}=6,8\)cm
AB2= BC.BH
=> BH= \(\frac{AB^2}{BC}\)= \(\frac{6^2}{10}\)
= 3,6 cm
AC2 = BC.CH
=> CH= \(\frac{AC^2}{BC}=\frac{8^2}{10}=6,4cm\)

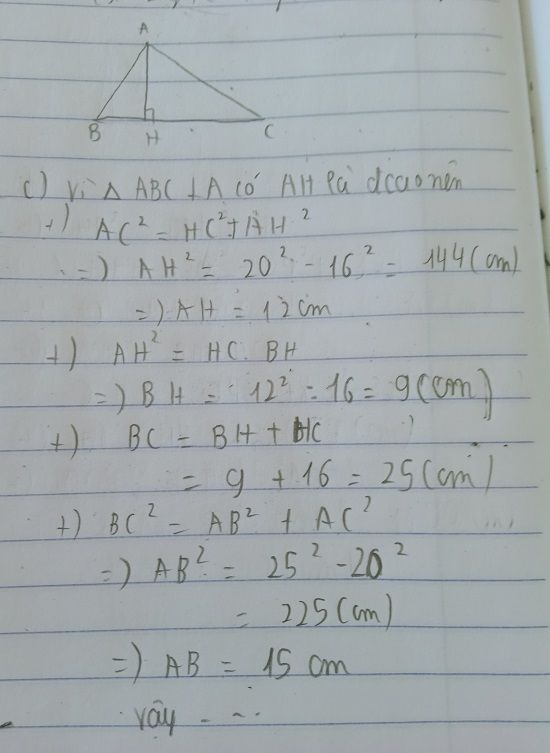
b) Xét tam giác ABC vuông tại A có AH là đường cao nên ta có:
A B 2 = BH.BC
⇒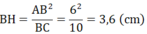
A C 2 = CH.BC
⇒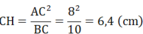
AH.BC = AB.AC
⇒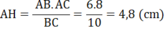
Vậy AH = 4,8 cm; BH = 3,6 cm; CH = 6,4 cm