Chứng minh rằng không có x;y nguyên nào thỏa mãn biểu thức sau :
1)x^2-y^2=1998
2)x^2+y^2=1999
Mk đang cần gấp!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để phương trình có nghiệm thì f(x)=0
⇔x2-2x+2016=0
⇔ (x-1)2+2015=0
⇔ (x-1)2=-2015 (vô lí do (x-1)2≥0)
Vậy,phương trình vô nghiệm
F(x)=x2−2x+2016F(x)
F(x)=x2−2x+1+2015
F(x)=x2−x−x+1+2015
=x(x−1)−(x−1)+2015
=(x−1)^2+2015
Vì (x−1)2+2015≥2015>0 với mọi x ∈ R
=>F(x) vô nghiệm (đpcm)


Q(x)=x4+2015x2+2016
có: x4\(\ge\)0 với mọi x
2015x2 \(\ge\)0 với mọi x
2016>0
=> x4+2015x2+2016>0
Q(x) ko có nghiệm

Lời giải:
Giả sử $P(x)$ có nghiệm $a$ nguyên. Khi đó:
$a^3-3a+5=0$
$\Leftrightarrow a(a^2-3)=-5$
Khi đó ta xét các TH sau:
TH1: $a=1; a^2-3=-5$
$\Leftrightarrow a=1$ và $a^2=2$ (vô lý)
TH2: $a=-1; a^2-3=5$
$\Leftrightarrow a=-1; a^2=8$ (vô lý)
TH3: $a=5; a^2-3=-1$
$\Leftrightarrow a=5$ và $a^2=2$ (vô lý)
TH4: $a=-5; a^2-3=1$
$\Leftrightarrow a=-5$ và $a^2=4$ (vô lý)
Vậy điều giả sử là sai, tức $P(x)$ không có nghiệm nguyên.

Ta có: \(x^2+4x+5=x^2+2x+2x+4+1\)
\(=\left(x^2+2x\right)+\left(2x+4\right)+1\)
\(=x\left(x+2\right)+2\left(x+2\right)+1\)
\(=\left(x+2\right)^2+1\)
Vì \(\left(x+2\right)^2\ge0\) nên \(\left(x+2\right)^2+1\ge1\)
Vậy đa thức trên ko có nghiệm
Chúc bạn học tốt !!!

Ta có: \(x^2-2x+2\) \(=x^2-2x+1+1\)
\(=\left(x^2-2x+1\right)+1\)
\(=\left(x-1\right)^2+1\)
Vì (x - 1)^2 \(\ge\) 0 nên (x - 1)^2 + 1 \(\ge\)1
Vậy đa thức trên ko có nghiệm
Ta có: x2 - 2x + 2 = x2 - 2x + 1 + 1 = (x - 1)2 + 1 \(\ge\)1
Vậy pt vô nghiệm

Chọn hai dãy số có số hạng tổng quát là 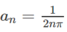 và
và 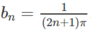 .
.
Tính và so sánh lim f ( a n ) và lim f ( b n ) để kết luận về giới hạn của f(x) khi x → 0

Lời giải:
$2M(x)=2x^4+2x^3+4x^2+2=x^4+(x^4+2x^3+x^2)+3x^2+2$
$=x^4+(x^2+x)^2+3x^2+2\geq 2>0$ với mọi $x$
$\Rightarrow M(x)>0$ với mọi $x$
$\Rightarrow$ đa thức $M(x)$ vô nghiệm.
1, Ta có: \(x^2-y^2=1998\Leftrightarrow\left(x-y\right)\left(x+y\right)=1998⋮2\Rightarrow\left(x-y\right)\left(x+y\right)⋮2\)
mà \(\left(x-y\right)+\left(x+y\right)=2y⋮2\Rightarrow x-y,x+y\)cùng tính chẵn lẻ suy ra \(x-y,x+y\)cùng chẵn
\(\Rightarrow\left(x-y\right)\left(x+y\right)⋮4\Rightarrow1998⋮4\)(vô lí) suy ra không tồn tại
2, gt => x,y khác tính chẵn lẻ. Giả sử x chẵn, y lẻ suy ra \(x=2k,y=2m+1\left(k,m\inℤ\right)\)
Khi đó: \(\left(2k\right)^2+\left(2m+1\right)^2=1999\Leftrightarrow4k^2+4m^2+4m+1=1999\Leftrightarrow1998=4\left(k^2+m^2+m\right)⋮4\)
\(\Rightarrow1998⋮4\)(vô lí) suy ra không tồn tại
Thanks bn iu!!!