Bài 4 Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Hai đường thẳng DE và BC cắt nhau tại F. Chứng minh rằng:a) Tứ giác BCDE nội tiếp.b)góc AFE= ACE.Bài 5. Cho nứa đường tròn đường kính AB. Lấy hai điểm C và D trên nửa đường tròn sao cho cung AC= cung CD= cung DB. Các tiếp tuyến vẽ từ B và C của nửa đường tròn cắt nhau tại I.Hai tia AC và BD cắt...
Đọc tiếp
Bài 4 Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Hai đường thẳng DE và BC cắt nhau tại F. Chứng minh rằng:
a) Tứ giác BCDE nội tiếp.
b)góc AFE= ACE.
Bài 5. Cho nứa đường tròn đường kính AB. Lấy hai điểm C và D trên nửa đường tròn sao cho cung AC= cung CD= cung DB. Các tiếp tuyến vẽ từ B và C của nửa đường tròn cắt nhau tại I.Hai tia AC và BD cắt nhau tại K. Chứng minh rằng:
a) Các tam giác KAB và IBC là những tam giác đêu.
b) Tứ giác KIBC nội tiếp.
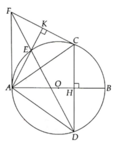
Bài 6. Cho nửa đường tròn (0) đường kính AB và tia tiếp tuyến Bx của nửa đường tròn. Trên tia Bx lấy hai điểm C và D (C nằm giữa B và D). Các tia AC và BD lần lượt cắt đường tròn tại E và F. Hai dây AE và BF cắt nhau tại M. Hai tia AF và BE cắt nhau tại N. Chứng minh rằng:
a) Tứ giác FNEM nội tiêp.
b) Tứ giác CDFE nội tiếp.
Bài 7. Cho tam giác ABC. Hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC.
a) Chứng minh rằng tứ giác ABDC nội tiếp được đường tròn. Xác định tâm 0 của đường tròn đó
b) Đường thẳng DH cắt đường tròn (0) tại điểm thứ hai là I. Chứng minh rằng năm điểm A, I, F, H, E cùng nằm trên một đường tròn
Các bạn giải giúp mình các bài này nhé, mình cảm ơn nhiều lắm

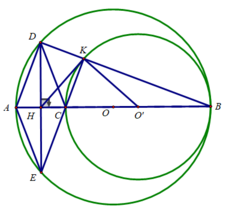
Gọi I là tâm đường tròn đường kính CB
a) Xét (O) có: \(\widehat{ADB}\) \(=90^0\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AD\perp DB\)
Xét (I) có: \(\widehat{CKB}\) \(=90^0\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow CK\perp KB\) hay \(CK\perp DB\)
Ta có: \(\widehat{DKC}+\widehat{CKB}\) \(=180^0\) (hai góc kề bù)
\(\Leftrightarrow\) \(\widehat{DKC}\) \(=180^0-\) \(\widehat{CKB}\) \(=180^0-90^0=90^0\)
Vì \(\widehat{ADB}+\widehat{DKC}\) \(=90^0+90^0=180^0\)
\(\Rightarrow\) Tứ giác DKCH nội tiếp đường tròn (theo dhnb tứ giác nội tiếp)
b) Vì H là trung điểm AC
\(\Rightarrow AH=HC\)
Xét (O) có: \(\left\{{}\begin{matrix}AB=2R\\DE\perp AB=\left\{H\right\}\end{matrix}\right.\)
\(\Rightarrow DH=HE\) (liên hệ giữa đường kính và dây)
Xét tứ giác ADCE có: \(\left\{{}\begin{matrix}DH=HE\\AH=HC\\DE\cap AC=\left\{H\right\}\end{matrix}\right.\)
\(\Rightarrow\) Tứ giác ADCE là hình bình hành (theo dhnb hình bình hành)
(mà \(DE\perp AC=\left\{H\right\}\))
\(\Rightarrow\) Hình bình hành ADCE là hình thoi (theo dhnb hình thoi)
\(\Rightarrow\) AD//EC (1)
Vì \(\left\{{}\begin{matrix}AD\perp DB\\CK\perp DB\end{matrix}\right.\) \(\Rightarrow\) AD//CK (từ vuông góc đến song song) (2)
Từ (1) và (2) \(\Rightarrow\) AD//EC//CK
\(\Rightarrow\) E,C,K thẳng hàng.
c) Vì \(DE\perp AC=\left\{H\right\}\)
\(\Rightarrow\) \(\widehat{DHA}\) \(=90^0\)
Vì AD//EC \(\Rightarrow\) \(\widehat{ACE}=\widehat{DAC}\) hay \(\widehat{DAH}=\widehat{HCE}\)
(mà \(\widehat{HCE}=\widehat{KCB}\) vì hai góc đối đỉnh)
\(\Rightarrow\) \(\widehat{DAH}=\widehat{KCB}\)
Xét ΔADH∼ΔCBK vì:
\(\widehat{DHA}=\widehat{CKB}\) \(=90^0\)
\(\widehat{DAH}=\widehat{KCB}\) (cmtrn)
\(\Rightarrow\frac{AD}{CB}=\frac{AH}{CK}\Leftrightarrow AD\cdot CK=AH\cdot CB\) (mà \(AH=HC\))
\(\Leftrightarrow AD\cdot CK=HC\cdot CB\) (đpcm)